
We’ve seen that the regular languages are those that have an accepting DFA.
Question: Are NFAs more powerful? In other words, are there languages that NFAs can accept that DFAs can’t?
If NFAs are no more powerful than DFAs, then things get a lot easier: for example, the following language from the Exercises is simply the union of two languages: \[ L = \{w : w \text{ contains an odd number of $a$'s or exactly two $b$'s}\} \]
and the approach that works to build an NFA from this (that is, joining each language’s DFA with an \(\epsilon\) transition from a shared start state) could work on any pair of languages!
It turns out that no, NFAs are not more powerful.
Exercises Part A - NFA design warmup
Theorem: For any NFA \(N\), there exists an equivalent DFA \(M\) such that \(L(M) = L(N)\).
Proof: Suppose \(N\) is an NFA \((Q, \Sigma, \delta, q, F)\). We show how to construct a DFA \(M = (Q', \Sigma', \delta', q', F')\) such that \(L(M) = L(N)\).
Here we will not give the formal proof in its full generality, but work through an example and convince ourselves that this approach works in general. The game plan here is to design a DFA that runs all possible computations that the NFA could run on the input. The process is somewhat similar to how we proved the union case for DFAs, except instead of each DFA state corresponding to pairs of original machine states, they will represent sets of states that the input machine might have been in.
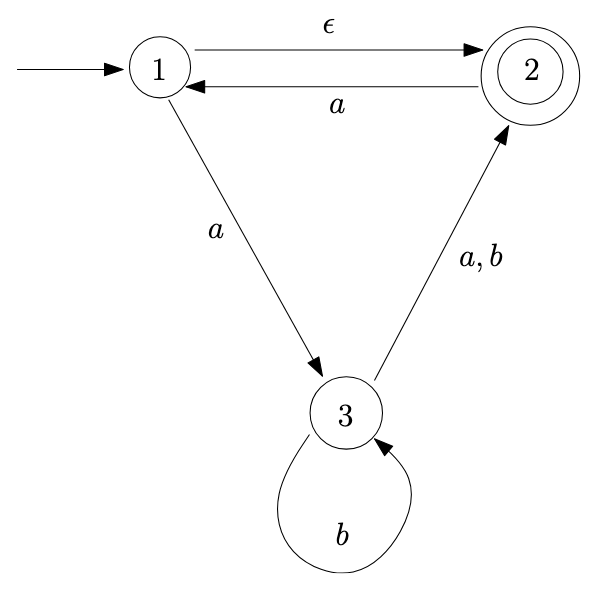
Consider the following NFA; for convenience, I’ve also included its transition table:


Do Exercises - Part B
As we saw in the exercises, the machine above could be in state 1 after reading \(aaa\) without any \(\epsilon\)-transitions. If we allow for \(\epsilon\)-transitions, then the machine could be in any of \(\{1, 2, 3\}\).
To help formalize this, we will define the following:
Definition: The \(\epsilon\)-closure of a state \(s\) ins \(Q\), denoted \(C_{\epsilon}(s)\) is the set of states reachable from \(s\) after 0 or more \(\epsilon\) transitions.
In the machine above, the \(\epsilon\)-closures are as follows:
We’ll now show, a little informally, how to convert an NFA to a DFA. See the whiteboard notes, and also Section 2.5 of TC. Section 2.5 gives the general process, while Section 2.5.1 shows the conversion for this example.
Let our NFA \(N = (Q, \Sigma, \delta, q, F)\).
Construct a DFA \(M = (Q', \Sigma, \delta', q', F')\) as follows:
The NFA states \(Q' = \mathcal{P}(Q)\) each correspond to a subset of the DFA states.
The start state \(q' = \{q\}\); we start in the state corresponding to the set containing only the NFA’s start state.
The accept states \(F'\) contains any state \(R \in Q'\) that contains least one NFA accept state: \[ F' = \{R \in Q' : R \cap F \ne \varnothing \} \]
The transition function simulates the running of the NFA from any of the current NFA states represented by the DFA state, yielding the new set of states the NFA could have been in after reading the next symbol. Formally, \[ \delta'(R, a) = \bigcup_{r \in R} \delta(r, a) \]
To simulate a machine as above with \(\epsilon\) transitions, we will need to account for the possibility that a machine follows one at any point during the reading of the string. We’ll simulate this in the following way:
A single “step” of the machine will now be a pair of these steps, by accounting for the \(\epsilon\) closure. We will set things up so that the transition function does a pair such as 2-3, that is, we will read a symbol and then make epsilon transitions.
To set this up, the start state needs to account for step 1; so now \(q' = C_\epsilon(q)\), and we’re set up for \(\delta'\) to read a symbol up front. So instead of the above, we have \[ \delta'(R, a) = \bigcup_{r \in R} C_{\epsilon}(\delta(r, a)) \] In words, this is “the union of the epsilon closure of all states that the NFA’s transition function could have sent us to from any of the states we may have been in”. Or in other words, if may have been in a given set of states \(R\), this sends us to a new set of states that we could have reached by reading one symbol and then making 0 or more epsilon transitions.
Do Exercises - Part C