CSCI 301 L20 Notes

Lecture 20 - Notes

Goals

• Be able to show that regular languages are closed under the union operation
• Know the definition of a nondeterministic finite automaton (NFA)
• Know how to determine if a string is accepted by an NFA, and the definition of the language accepted by an NFA

Announcements

• At the end of class

The Regular Languages are closed under the regular operations

Regular Operations

Recall we defined the following operations on languages:

• The union of two languages \(A\) and \(B\) is defined as \(A \cup B = \{w : w \in A \text{ or } w \in B\}\).
• The concatenation or product of two languages \(A\) and \(B\) is defined as \(AB = \{ww' : w \in A \text{ and } w' \in B\}\).
• The closure or star (or Kleene closure) of a language \(A\) is defined as: \(A^* = \{u_1 u_2 \ldots u_k : k \ge 0 \text{ and } u_i \in A \text{ for all } i = 1, 2, \ldots, k\}\)
  • In other words, it’s the language containing all possible concatenations of any choice of 0 or more strings over \(A\). Notice that 0 is an option here, so \(\epsilon \in A^*\) for any language \(A\).
  • Another equivalent recursive definition is:
    • Let \(A^0 = \{\epsilon\}\)
    • Let \(A^k = AA^{k-1}\)
    • \(A^* = \bigcup_{k=0}^{\infty} A^k\)

Theorem: The set of regular languages is closed under the regular operations. That is, applying any of the regular operations to regular languages produces only languages that are also regular.

Proof: Not yet. We don’t have the tools to prove this in full yet, but we’ll work through an example that gives us some intuition for how this could be shown for the union operation:

Consider the following two languages \(L_A\) and \(L_B\) over \(\Sigma = \{0, 1\}\):

• \(L_A = \{w : |w| \text{ is even} \}\)
• \(L_B = \{w : w \text{ ends with a $1$} \}\)

First, to prove that these languages are regular, we can show that there exist DFAs \(M_A\) and \(M_B\), where \(L(M_A) = A\) and \(L(M_B) = B\).

We did this in the Exercises:

Then, to show that \(L_A \cup L_B\) is regular, we must show that there exists a DFA \(M_{A \cup B}\) such that \(L(M_{A \cup B}) = L_A \cup L_B\).

Brainstorm: How could we do this?

(See the handwritten notes for a DFA accepting \(L_A \cup L_B\))

The general procedure is this:

• The set of states is \(Q_A \times Q_b\)

• The start state is the state \((q_A, q_B)\)

• The accept states are \(\{(s_A, s_B) : s_A \in F_A \text{ or } s_B \in F_B\}\)

• The transition function is defined by:

  • \(\delta_{A \cup B} ((s_A, s_B), x) = (\delta_A(s_A, x), \delta_B(s_B, x))\)

    In other words, the transition function takes you from the pair of states you’re at to the pair of states the two individual machines would be in after they each saw the next symbol.

So we’ve seen (informally) that the union of two regular languages is a regular language.

What about the other regular operations?

Proving this property for concatenation and the closure (star) operations is a little trickier, so we’re going to take a detour that will make it much simpler: next we’re going to introduce nondeterministic finite automata, which are much easier to work with and combine. Then, the plot twist is that NFAs aren’t any more powerful than DFAs - meaning that anything an NFA can do, a DFA can also do.

Nondeterministic Finite Automata

Let’s break some rules. Suppose we want to find a FA that accepts all strings containing either 1011 or 000 as a substring. I’m going to make a FA for this, but it’s not going to follow the rules for a DFA.

(see the handwriten notes for the NFA)

What rules did we break?

• We transitioned from one state to the next without reading a character
• The transition function maps a (state, symbol) pair to zero or more other states

How do we define this new machine mathematically? An NFA is almost the same as a DFA, with two differences:

• For strings over an alphabet \(\Sigma\), an NFA’s alphabet is defined as \(\Sigma \cup \{\epsilon\}\).

• The transition function was previously:

  • \(\delta : Q \times \Sigma \rightarrow Q\), and is now instead defined as
  • \(\delta : Q \times \Sigma \rightarrow \mathcal{P}(Q)\)

  That is, a (state, symbol) pair can now map to zero or more states.

This introduces ambiguity, so which strings do we say are accepted? We say that an NFA accepts a string if there is any sequence of state transitions possible that result in an accept state.

Do Exercises Part A-B

Medium-Large Question

We’ve seen that the regular languages are those that have an accepting DFA. Are NFAs more powerful? In other words, are there languages that NFAs can accept that DFAs can’t?

If NFAs are no more powerful than DFAs, then things get a lot easier: for example, the following language from the Exercises is simply the union of two languages:

\[ L = \{w : w \text{ contains an odd number of $a$'s or exactly two $b$'s}\} \]

and the approach that works to build an NFA from this (that is, joining each language’s DFA with an \(\epsilon\) transition from a shared start state) could work on any pair of languages.

It turns out that no, NFAs are not more powerful.

Theorem: For any NFA \(N\), there exists an equivalent DFA \(M\) such that \(L(M) = L(N)\).

We can prove this by taking an NFA and constructing a DFA that accepts the same language. We won’t do this in full formality or generality, but we will work through an example conversion and show that it generalizes. The process is somewhat similar to how we proved the union case for DFAs, except instead of constructed DFA state corresponging to pairs of original machine states, we’ll need to represent sets of states that the input machine might have been in.

Announcements

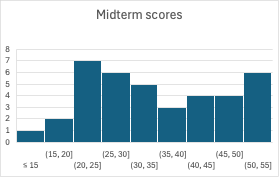
Midterms are graded. It was not an easy exam! Here is the distribution of scores (out of 60):

Exam Wrapper

You have an opportunity to earn some points back by completing a midterm exam wrapper, in which you’ll analyze your mistakes and reflect on your study strategies. The number of points you can earn back depends on your original score. You’ll submit on Canvas; the assignment is up, and submissions are due a week from tonight. The writeup with details is here, and also linked from the Midterm day on the Schedule table.

Final Exam Score Replacement Policy

As a reminder:

If your final exam grade exceeds your midterm exam grade, then your midterm exam grade will be replaced by your final exam grade in the calculation of your final grade.

This applies after any adjustments made due to the exam wrapper.

Gradescope

I’ll release the scores after class. I grade and return the exams using a tool called Gradescope. You’ll get an email saying your exam is graded. To view it (since this is your first assignment in this class), you’ll need to:

• Click the “set your password” link in the email and “reset your password” (even though you never had one in the first place)

• Log in with your WWU email and the password you set to see your exam and feedback.

• When looking at feedback you’ll see something like this:

  

  Questions are scored on rubrics; note that you can see all of the rubric items, but only the ones highlighted with a checkmark are the ones that were applied to your solution.

Grades will be released via Gradescope today; scores will be released on Canvas in about a week.