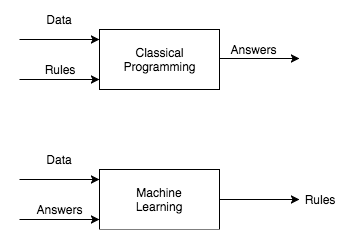
Lecture 16 - Machine Learning: Intro/Overview; Vectors and Distances¶

In [ ]:

Announcements:¶

Goals:¶

  • See a few different perspectives on "what is machine learning?"
    • CS/programmer's perspective
    • DS/data wrangler's perspective
    • Stats/mathematician's perspective
  • Know the basic mathematical setup of most machine learning methods.
  • Be able to give some example use cases where machine learning is the best, if not only practical, way to solve a computing problem.
  • Know how to represent datapoints as vectors, and how to compute $L_p$ distances between them.

What the heck is ~all this hype~ machine learning about?¶

A programmer's perspective:¶

It's a tool that we can use when we don't know how to just write the code to compute the answer.

A data scientist's perspective:¶

A way to discover underlying structure in data that allows us to:

  • Better understand the world that generated the data
  • Predict values (columns, rows, subsets thereof) that are:
    • missing (imputation), or
    • haven't happened yet (prediction, time series forecasting, etc.)

A mathematical / probabilistic perspective:¶

Given a set of data $X$ and (possibly) labels $y$ (i.e., quantities to predict), model one or more of the following:

  • $P(x)$
  • $P(y \mid x)$
  • $P(x, y)$.

Math Fact: If you know $P(x, y)$, you can compute $P(y \mid x)$ and $P(x)$:

$$P(y \mid x) = \frac{P(x, y)}{P(x)}$$ and $$P(x) = \sum_i P(x,y_i)$$

Machine Learning: When and Why?¶

  • We don't know the underlying process that generated the data, but we have examples of its outputs
  • Use cases: (so far) data-rich domains with problems we don't know how to solve any other way.
  • High-profile examples are from complex domains:
    • Speech recognition
    • Image recognition / object detection
    • Weather forecasting
    • Natural Language Processing
    • Self-driving cars (robotics)
    • Drug design

Side note: Machine Learning vs. Artificial Intelligence¶

  • AI is the study of making computer systems behave with "intelligence" (what does that mean?)
  • ML is generally considered a subfield of AI
    • ML has come the closest so far to exhibiting intelligent behavior
    • Actively debated: is ML the way to "general" AI?
    • In current usage, "AI" almost exclusively refers to ML-based methods

Supervised vs Unsupervised¶

Supervised Learning, by example:

  • $X$ is a collection of $n$ homes with $d$ numbers about each one (square feet, # bedrooms, ...); $\mathbf{y}$ is the list of market values of each home.

Key property: a dataset $X$ with corresponding "ground truth" labels $\mathbf{y}$ is available, and we want be able to to predict a $y$ given a new $\mathbf{x}$.

Unsupervised Learning, by example:

  • Same setup, but instead of predicting $y$ for a new $\mathbf{x}$, you want to know which of the $d$ variables most heavily influences home price.

Key property: you aren't given "the right answer" - you're looking to discover structure in the data.

In [ ]:
import seaborn as sns
import numpy as np

Feature Extraction¶

The vast majority of machine learning methods assume each of your input datapoints is represented by a feature vector.

If it's not, it's usually your job to make it so - this is called feature extraction. mk Given a DataFrame, we can treat each row as the feature vector for the thing the row describes. Traditionally, we arrange our dataset in an $N \times D$ matrix, where each row corresponds to a datapoint and each column corresponds to a single feature (variable). This is the same layout as a pandas table.

If your input is an audio signal, a sentence of text, an image, or some other not-obviously-vector-like thing, there may be more work to do.

Given a dataframe like the penguins dataset, it's pretty easy to get to a ML-style training dataset X, y:

In [ ]:
penguins = sns.load_dataset("penguins")
sns.relplot(data=penguins, x="flipper_length_mm", y="bill_length_mm")
In [ ]:
X = penguins[["flipper_length_mm", "bill_length_mm"]].to_numpy()
X.shape
In [ ]:
X[:10,:]
In [ ]:
penguins["species"].value_counts()
In [ ]:
y = penguins["species"].map({"Gentoo": 1, "Adelie": 2, "Chinstrap": 3}).to_numpy()
y.shape
In [ ]:
y
In [ ]:

Distance Metrics¶

So you have your datapoints represented as vectors. The big thing this enables is for us to compare two datapoints numerically - this is done by computing a disance (or inversely, similarity) between two datapoints.

$L^p$ Distances¶

A common family of distance metrics is the $L^p$ distance:

$$d_p(a, b) = \sqrt[p]{\sum_{i=1}^d |a_i - b_i|^p}$$

When $p = 2$, this is the Euclidean distance we're all used to, based on the Pythagorean theorem; in 2D, it reduces to: $$\sqrt{(b_x - a_x)^2 + (b_y - a_y^2)}$$

Different values of $p$ give different behavior:

  • For smaller $p$, we care less about how different the per-dimension differences are from each other.
  • For larger $p$, we care more about how different the per-dimension differences are from each other.

A few examples of the "unit circle" under different $L^p$ distances:

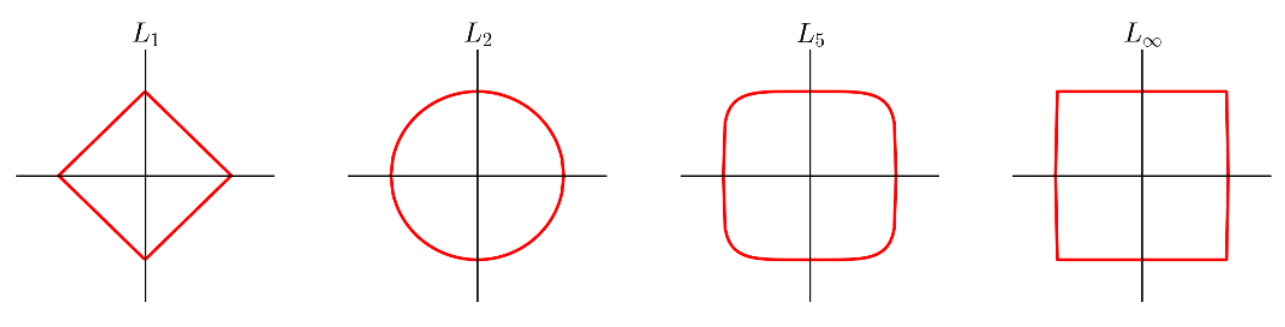
$L_1$ and $L_2$ are by far the most common choices here.

Exercise: rank the penguins by similarity to Penguin 0, based on an L2 distance between flipper + bill length vectors.

In [ ]:
X[0]
In [ ]:
penguins.iloc[0,:]
In [ ]:

More Distance Metrics¶

Hamming Distance¶

For vectors of categorical values, Hamming distance is the number of dimensions in which two vectors differ: $$d(a, b) = \sum_i \mathbb{1}(a_i \ne b_i)$$ where $\mathbb{1}(\cdot)$ is an indicator function that has value 1 if its argument is true and 0 otherwise.

Cosine Similarity¶

A similarity (not distance) metric that considers only vector direction, not magnitude:

$$ sim(a, b) = \cos \theta = \frac{a^Tb}{\sqrt{(a^Ta)(b^Tb)}}$$