Lecture 17 - Machine Learning - The In-Distribution Assumption; Generalization

import pandas as pd
import seaborn as sns

df = pd.DataFrame({
  "Income": [0.49, 0.18, 0.31, 0.40, 0.24],
  "CrimeRate": [0.09, 0.45, 0.23, 0.19, 0.48]
})

Announcements:

• Quiz 4 - the multiple-answer numpy question has been regraded.
• Quiz 5 grading complete.

Goals:

• Understand the near-universal assumption of machine learning models: unseen data is drawn from the same distribution as the training dataset, and the implications of this assumption.
• Know how true risk differs from empirical risk.
• Know how to define bias, variance, irreducible error.
• Be able to identify the most common causes of the above types of error, and explain how they relate to generalization, risk, overfitting, underfitting.
• Know why and how to create separate validation and test sets to evaluate a model

Machine Learning: Foundational Assumptions

The In-Distribution Assumption

Generally: unseen data is drawn from the same distrubtion as your dataset.

Consequence: We don't assume correlation is causation, but we do assume that observed correlations will hold in unseen data.

Model-Specific Assumptions

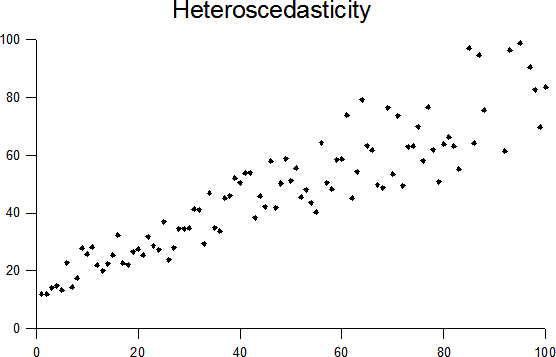
Specific model classes make additional assumptions. For example, linear regression assumes:

• Columns are linearly independent (i.e., one column can't be directly computed from another
• Data is homoscedastic, i.e., the following won't happen:

Big Idea: Generalization

Generalization is the ability of a model to perform well on unseen data (i.e., data that was not in the training set).

• As discussed above: we're usually hoping to perform well on unseen data that is drawn from the same distribution as the training set.

sns.scatterplot(data=df,x="Income",y="CrimeRate")

<matplotlib.axes._subplots.AxesSubplot at 0x7fa922a7f3a0>

Consider the following possible model classes:

• Linear functions (degree-1 polynomials)
• Quadratic functions (degree-2 polynomials)
• Degree-10 polynomials

Question 1: Which of these chioces of model class will result in the best (lowest) empirical risk $\hat{R}(h; \mathcal{X})$?

Question 2: Which of these will result in the best (lowest) empirical risk on another batch of data $\mathcal{X}'$ drawn from the same distribution as $\mathcal{X}$?

• In other words, which of these will generalize best?

Empirical Risk vs True Risk

Let's formalize the above distinction.

What we truly care about is a quantity known as (true) risk: $R(h; {\cal X})$.

• True risk is the expected loss "in the wild"
• Depends on a probability distribution that we don't know: $P(x,y)$ -- the joint distribution of inputs and outputs.
  • If we knew $P$, there's nothing left to "learn": let $\hat{y} = \arg\max_y P(y | x)$.

Where does risk come from?

There are three contributors to risk:

1. Bias (not the same bias as the $b$ in our linear model)
2. Variance
3. Irrereducible error

To understand bias and variance, we need to consider hypothetical:

• There is some underlying distribution/source generating input-output pairs
  • The probabily of a pair is denoted $P(x,y)$
  • The probability of the output given the input is denoted $P(y|x)$
  • Why a distribution? Because the same input (x) can have different ouputs (y).
    • Example: x contains home features: square feet, # bedrooms. Many houses are 2400 square feet with 3 bedrooms, and they're not all priced the same.
• for i in 1..K
  • Get a random training set with $N$ points sampled from $P$
  • Train a model on that training set, call that $h_i(x)$.
• Define $\bar{h}(x) = \frac{1}{K} \sum_{i=1}^K h_i(x)$

Bias

• The bias of the training process is how far $\bar{h}(x)$ is from the mean of $P(y|x)$.
• High bias implies something is keeping you from capturing true behavior of the source.
• Most common cause of bias? The model class is too restrictive aka too simple aka not powerful enough aka not expressive enough.
  • E.g., if the true relationship is quadratic, using linear functions will have high bias.
• Training processes with high bias are prone to underfitting.
  • Underfitting is when you fail to capture important phenomena in the input-output relationship, leading to higher risk.

Variance

• The variance of a training process is the variance of the individual models $h_i(x)$; that is, how spread they are around $\bar{h}(x)$.
• This is a problem, because we only have one $h_i$, not $\bar{h}(x)$, so our model might be way off even if the average is good.
• Most common causes of variance?
  • Too powerful/expressive of a model, which is capable of overfitting the the training. Overfitting means memorizing or being overly influenced by noise in the training set.
  • Small training set sizes ($N$).
  • Higher irreducible error (noisier training set).

Irreducible Error

• Even if you have a zero bias, zero variance training process, you then predict the mean $P(y|x)$, which is almost never right.
  • Because the truth is non-deterministic.
  • This error that remains is the irreducible error.
• Source of irreducible error?
  • Not having enough, or enough relevant features in $x$.
• Note: this error is only irreducible for a given feature set (the information in $x$). If you change the problem to include more features, you can reduce irreducible error.

Worksheet: Problems 1 - 4

Identifying the model with the best generalization (i.e. lowest true risk)

• Answer: hold out a test set. Use this to estimate (true) risk.
• So we need a training set and a test set. But that is not enough in practice. Why?
  • The more times you see results on the test set, the less representative it is as an estimate for $R$.
  • Example: 10k random "models"
• We need a training set, a test set, and ideally a development or validation set.
  • This set is a surrogate for the test set.