Lecture $2^5$ - Evaluating Classifiers

Announcements:

• Instructions for Milestone 1 writeup are up on the FP webpage

Goals

• Know how to understand the performance of binary classifiers:
  • The definition of True/False Positives/Negatives
  • The calculation of different performance metrics, including:
    • accuracy
    • precision
    • recall
    • F-score
  • Know how to interpret a Receiver-Operator Characteristic (ROC) curve
• Know how to understand the performance of multiclass classifiers:
  • Top-$k$ accuracy
  • Confusion matrix

Binary Classification

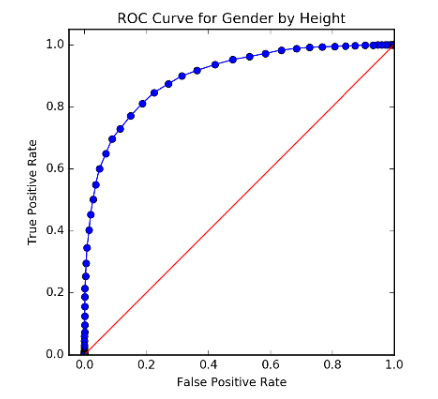
This is trickier than regression, and the reason is that most intuitive metrics can be gamed using a well-chosen baseline.

Simplest metric - accuracy: on what % of the examples were you correct?

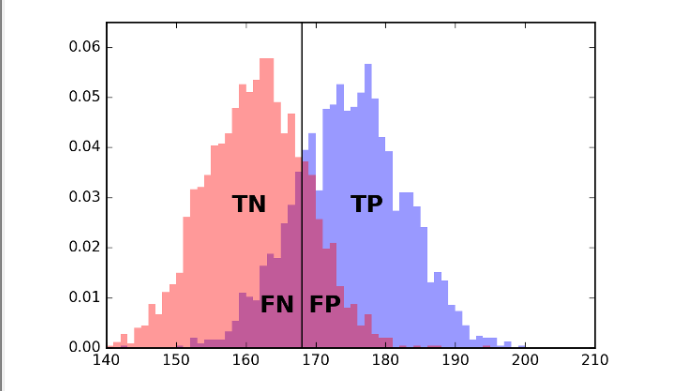
There are different kinds of right and wrong:

• TP - True positives (correctly labeled positive)
• TN - True negatives (correctly labeled negative)
• FP - False positives (incorrectly labeled positive; was actually negative)
• FN - False negatives (incorrectly labeled negative; was actually positive)

Exercise: let TP be the number of true positives, and so on for the other three. Define accuracy in terms of these quantities.

Accuracy = $\frac{TP + TN}{TP + TN + FP + FN}$

Exercise: Game this metric. Hint: suppose the classes are unbalanced (95% no-tumor, 5% tumor).

Okay, what's really important is how often you're right when you say it's positive:

Exercise: define a metric that captures this.

Precision = $\frac{TP}{TP + FP}$

Anything wrong with this? Hint: there is cancer involved.

Okay, what's really important is how often you miss a real case of cancer.

the fraction of real cancer cases that you correctly identify.

Exercise: define a metric that captures this.

Recall = $\frac{TP}{(TP + FN)}$

Exercise: Game this metric.

Can't we just have one number? Sort of. Here's one that's hard to game:

F-score $= 2 *\frac{\textrm{precision } * \textrm{ recall}}{\textrm{precision } + \textrm{ recall}}$

Tuning a Binary Classifier

Sometimes your classifier will have a built-in threshold that you can tune. The simplest example is a simple threshold classifier that says "positive" if a single input feature exceeds some value, and negative otherwise.

Consider trying to predict sex (Male or Female) given height:

If you move the line left or right, you can trade off between error types (FP and FN).

The possibilities in this space of trade-offs can be summarized by plotting FP vs TP:

Edited to add:

• "True Positive Rate" = $\frac{TP}{TP+FN}$, the fraction of datapoints with positive ground truth labels that were true positives (this is the same as recall!)
• "False Positive Rate" = $\frac{FP}{FP + TN}$, the fraction of datapoints with negative ground truth labels that were false positives.

Exercise:

• What would the ROC curve of a perfect classifier look like?
• What would the ROC curve for a random-guess baseline look like?

Multi-Class Classification

Usually, a multiclass classifier will output a score or probability for each class; the prediction will then be the one with the highest score or probability.

Metrics:

• Accuracy - still possible, but random guess baseline gets worse fast, and good accuracy is very hard to get with many classes.
• Top-k accuracy: does the correct class lie in the $k$ most likely classes? Easier, and gives "partial credit"
• Precision and recall can be defined for each class:
  • Precision for class $c$: $\frac{\textrm{# correctly labeld } c}{\textrm{# labeled class } c}$
  • Recall for class $c$: $\frac{\textrm{# correctly labeled } c}{\textrm{# with true label } c}$

The full details can be represented using a confusion matrix: