Lecture 24 - Distance Metrics, Dimensionality Reduction, and Clustering

Announcements:

Goals (likely continuing into tomorrow):

Geometric Interpretation of Datapoints

Thinking in High-Dimensional Space

This is hard, and our intuition tends to fall apart. However, real high-dimensional data often lies on a lower-dimensional manifold.

What the heck does that mean?

If you sliced, rotated, projected, warped, etc. your space in just the right ways, you could represent the same information with fewer dimensions. The smallest possible number of dimensions possible to represent your data is called its intrinsic dimensionality.

Unsupervised Learning

Goal: discover structure without any ground-truth labels.

What might we mean by structure?

Dimensionality Reduction

Ways to get your $n$ feature vectors from $d$ dimensions to $d'$ dimensions (where $d' < d$).

Good for:

in all cases, these likely come at the expense of some accuracy.

Here are two common approches that are limited to linear notions of stretching, slicing, warping, etc:

Principal Components Analysis

Reduces dimensionality by finding $d'$ new features (each is a linear combination of the old features) that explain as much variance as possible.

Random Projections

Reduces dimensionality by multiplying $X_{n \times d}$ by a random matrix $P_{d \times d'}$, resulting in a reduced-dimensionality dataset $X'_{n \times d'}$.

Huh?

Somewhat surprisingly, this works pretty well. What's our metric for "works"? It preserves pairwise distances between points.

Distance Metrics

A common family of distance metrics is the $L^p$ distance:

$$d_p(a, b) = \sqrt[p]{\sum_{i=1}^d |a_i - b_i|^p}$$

When $p = 2$, this is the Euclidean distance we're all used to, based on the Pythagorean theorem; in 2D, it reduces to: $$\sqrt{(b_x - a_x)^2 + (b_y - a_y)^2}$$

Different values of $p$ give different behavior:

A few examples of the "unit circle" under different $L^p$ distances:

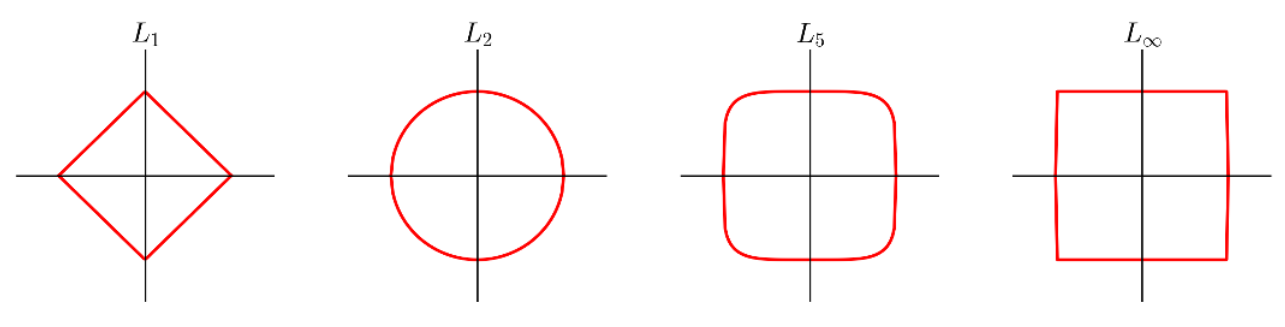
The curse of dimensionality, very briefly

It's worth noting that these distances become less and less useful as $d$ gets larger. There are a few ways to think about this, but the simplest is just that more dimensions means more opportunities for points to be far apart.