Lecture 8 - Conditional Probability, Independence, and Prediction

Goals:

• Know the definition and implications of independence
  • Know the definition of have intuition for conditional probability
  • Wrongly assuming independence can lead to poor modeling/predictions
  • A lack of independence leads to correlations, which is where modeling/predictive power comes from
• Understand how to interpret variances in general distributions and Gaussian (bell-shaped) distributions

Conditional Probability and Independence

Simple probability experiments like rolling two dice produce math that's friendly and easy to work with. The outcome of one die doesn't affect the outcome of the other.

Real life is rarely so simple.

A joint probability distribution on two random variables $P(X, Y)$ is the probability of each possible combination of values of $X$ and $Y$.

If $X$ is the number on the first die and $Y$ is the number on the second die, $P(X,Y)$ has a friendly property: $$P(X, Y) = P(X) P(Y)$$

Let's see why with our physically-improbable three-sided dice (written notes).

In convincing ourselves of the above properly, we sneakily started talking about conditional probability: a probability of something given that you know something else. In our dice example, the probability of die 2 being 1 given that die1 was a 1 was $1/3$. We write this in math as: $$P(Y=1 | X = 1) = 1/3$$ where the vertical bar $|$ is read as "given", or "conditioned on".

Independence is the property we described above: two events are independent if the outcome of one event doesn't affect, or change our understanding of the probability of another.

Another way to view independence is that the conditional probability is equal to the unconditional probability. For example, $$P(Y = 1 | X = 1) = 1/3 = P(Y = 1)$$ The information that $X = 1$ doesn't add anything to our understanding of the situation.

When are events not independent? Most of the time.

An abstract, probability-theory-type example might be: you flip a fair coin; if that fair coin is heads, you roll a fair three-sided die, but if it's tails you roll a weighted three-sided die whose odds of coming up 1 are 0.6, while the odds coming up 2 or 3 are 0.2 each.

Exercise 1: Let $C$ be the outcome of the coin flip and $D$ be the outcome of the die roll. write down the full joint distribution $P(C, D)$ for this experiment. I've given you the first one: $$P(C=H, D=1) = 1/6\\ P(C=H, D=2) = \hspace{1.6em}\\ P(C=H, D=3) = \hspace{1.6em}\\ P(C=T, D=1) = \hspace{1.6em}\\ P(C=T, D=2) = \hspace{1.6em}\\ P(C=T, D=3) = \hspace{1.6em}$$

Exercise 2: What is $P(D=1 | C=T)$?

Exercise 3: What is $P(D=1)$?

Less abstractly...

A fundamental assumption that data scientists implicitly make is that their data is generated by some process that follows the laws of probability. Let's look at our NHANES dataset from last time and think about these concepts in terms of some of the columns therein.

import pandas as pd
data_url = "https://fw.cs.wwu.edu/~wehrwes/courses/data311_21f/data/NHANES/NHANES.csv"
cols_renamed = {"SEQN": "SEQN",
                "RIAGENDR": "Gender", # 1 = M, 2 = F
                "RIDAGEYR": "Age", # years
                "BMXWT": "Weight", # kg
                "BMXHT": "Height", # cm
                "BMXLEG": "Leg", # cm
                "BMXARML": "Arm", # cm
                "BMXARMC": "Arm Cir", # cm
                "BMXWAIST": "Waist Cir"} # cm

df = pd.read_csv(data_url)
df = df.rename(cols_renamed, axis='columns')
df = df.drop("SEQN", axis='columns')

Remember that histograms are like empircal estimates of probability distributions. If we think of two columns as random variables of the outcomes of an experiment in which "A human grows to be an adult", we can similarly about the empirical estimate of the joint probability distribution, whether the columns are independent, and the conditional probability of one column's value given the other.

First, let's filter out children:

df = df[df["Age"] >= 21]

Now let's consider the age and height columns. I'm going to use a nifty visualization from the Seaborn library, which we'll use when we dig deeper into visualization:

import seaborn as sns

sns.jointplot(x="Age", y="Height", data=df)

<seaborn.axisgrid.JointGrid at 0x171be74f0>

From the scatter plot, it doesn't appear that these variables have much to do with each other. This matches our intuition - once they reach adulthood, people don't grow or shrink (much) in height as they age. This leads to a hypothesis that these variables are independent. We can think about this in terms of conditional probability by seeing if the distribution of heights conditioned on each age is the same as the unconditional distribution.

The following plot shows our empirical estimate of $P($Height$)$ alongside an empirical estimate of $P($Height $|$ the person is in their 20s$)$:

df["Height"].plot.hist(legend=True, label="P(Height)", density=True)
twenties = df[(df["Age"] >= 21) & (df["Age"] < 30)]
twenties["Height"].plot.hist(legend=True, label="P(height|20s)", density=True)

<AxesSubplot:ylabel='Frequency'>

The density=True argument tells the plotting library to divide by the total so instead of counts, we get probability-like values that all sum to one. This allows the $y$ axis scale to be comparable across two histograms of different total values.

Let's pick a different pair of columns and do a similar analysis:

sns.jointplot(x="Height", y="Leg", data=df)

<seaborn.axisgrid.JointGrid at 0x17194f820>

df["Leg"].plot.hist(legend=True, label="P(Leg)", density=True)

<AxesSubplot:ylabel='Frequency'>

for height in [140, 160, 180]:
    mask = (df["Height"] >= height) & (df["Height"] < height+20)
    label = f"P(Leg | {height} <= Ht < {height+20})"
    df[mask]["Leg"].plot.hist(legend=True, label=label,  density=True)

These columns are decidedly not independent! There is a strong correlation between them (we'll come back to that word and use it more formally later on). In other words, $P(Leg | Height) \ne P(Leg)$. That means that if we know Height, we have a better idea of what to expect from Leg. This forms the basis of our ability to make predictions from data!

The key insight I want you to take away from this is that the presence of correlations - aka a lack of independence - in the data yield predictive power. Two implications:

• If there are no correlations, we're unlikely to be able to make predictions.
• The correlation between leg length and height is clearly due to a real, underlying relationship between height and leg length. Not all correlations are, though! It's important to keep in mind that when we find a correlation, we have only failed to rule out the possibility a causal relationship between the two variables; but we have not confirmed its existence. In other words: correlation does not imply causation.

Interpreting Variance

Imagine a hypothetical prediction system where we wish to predict leg length given height. A sensible approach might be to predict the mean of the conditional distribution corresponding to the person's height (or height range). If we want to convey how confident we are in our prediction? Let's give the standard deviation as well.

If you're a consumer of that prediction, what do you now know?

• Of people that height, the average height is the prediction.
• How far off is the prediction likely to be?

A neat bit of mathematics is able to prove the following result:

For any probability distribution, at least the fraction $1 - \frac{1}{k^2}$ of the samples lie within $k$ standard deviations $(\sigma)$ of the mean. That is:

• $1 - 1/1^2 = 0$% within $1\sigma$
• $1 - 1/2^2 = 75$% within $2 \sigma$
• $1 - 1/3^2 = 89$% within $3\sigma$

For a Gaussian distribution (a particular bell-shaped curve), it gets a lot better than that:

• 68% are within $1 \sigma$
• 95% are within $2 \sigma$
• 99.7% are within $3 \sigma$

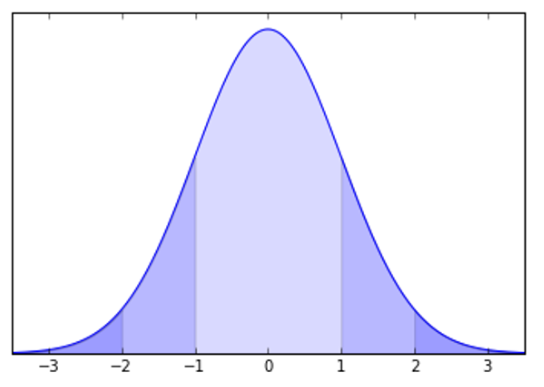
Even if your distribution is not precisely Gaussian (whatever that means) it is generally the case that the more "bell-shaped" your distribution, the closer your data will be to satisfying the bounds above for a Gaussian distribution.