Get a feel for some of the image processing operations that can and can't be accomplished using linear filtering.
Know the properties of the convolution and cross-correlation, and some of their implications:
Syllabus questions
Revisiting image formation: image noise
Noise as motivation for neighborhood operations
Live code: mean filter
Edge handling choices:
Write down the discrete math definition; aside: write down the continuous definition
Live code: generalize to cross-correlation with filter weights
Mess with the filter weights:
Exercise: compute a small cross-correlation result
Break
More filter weights:
Convolution vs cross-correlation
Properties - shift invariance; linearity; commutativity; associativity
Filter composition using associativity
Tricks using these properties:
# boilerplate setup
%load_ext autoreload
%autoreload 2
import os
import sys
src_path = os.path.abspath("../src")
if (src_path not in sys.path):
sys.path.insert(0, src_path)
# Library imports
import numpy as np
import imageio.v3 as imageio
import matplotlib.pyplot as plt
import skimage as skim
import cv2
# codebase imports
import util
import filtering
Let's make beans a little noisy.
# don't worry about the details here, we're just adding noise to beans
beans = imageio.imread("../data/beans.jpg")
bg = skim.color.rgb2gray(beans)
bg = skim.transform.rescale(bg, 0.25, anti_aliasing=True)
bn = bg + np.random.randn(*bg.shape) * 0.05
plt.imshow(bn, cmap="gray")
<matplotlib.image.AxesImage at 0x7fe17fcede90>
If each pixel measurement is corrupted, how can we improve our guess at what the "ideal" image should have been?
Idea: mean filter
Live-pseudocode:
def mean_filter(img, filter_size):
""" Apply a square spatial mean filter with side length filter_size
to a grayscale img. Preconditions:
- img is a grayscale (2d) float image
- filter_size is odd """
H, W = img.shape
hw = filter_size // 2
for i in range(H):
for j in range(W):
total = 0.0
for ioff in range(-hw, hw+1):
for joff in range(-hw, hw+1):
total += img[i + ioff, j + joff]
out[i,j] = total / filter_size**2
# Look at mean_filter
plt.imshow(filtering.mean_filter(bn, 5), cmap="gray")
<matplotlib.image.AxesImage at 0x7fe17f657cd0>
(whiteboard)
Edge handling:
Output size:
For anything but valid, how do you handle when the filter hangs over the void?
Another example
sticks = skim.color.rgb2gray(imageio.imread("sticks.png"))
plt.imshow(sticks, cmap="gray")
<matplotlib.image.AxesImage at 0x7fe17f6d6f10>
plt.imshow(filtering.mean_filter(sticks, 9), cmap="gray")
<matplotlib.image.AxesImage at 0x7fe17fcedf50>
See the lattice-like artifacts? Ick. Why is this happening?
Alternatives?
Here's one:
plt.imshow(cv2.GaussianBlur(sticks, ksize=(9,9), sigmaX=2), cmap="gray")
<matplotlib.image.AxesImage at 0x7fe17ddb7010>
TODO: implement filtering.filter
# test out the case of the mean filter we've been using
f = np.ones((9,9)) / (9*9)
plt.imshow(filtering.filter(sticks, f), cmap="gray")
<matplotlib.image.AxesImage at 0x7fe17f8e9e50>
# don't look behind the curtain!
g = np.zeros((9, 9))
g[4,4] = 1
g = cv2.GaussianBlur(g, ksize=(9, 9), sigmaX=2)
g /= g.sum()
plt.imshow(filtering.filter(sticks, g), cmap="gray")
<matplotlib.image.AxesImage at 0x7fe17dd35e90>
plt.imshow(f, cmap="gray")
plt.colorbar()
<matplotlib.colorbar.Colorbar at 0x7fe17dc1ddd0>
plt.imshow(g, cmap="gray")
<matplotlib.image.AxesImage at 0x7fe17da0c5d0>
where:
Practicalities when calculating this in real life:
(1) $f \otimes w$ indicates the cross-correlation of image $f$ with filter $w$. Compute the following cross-correlation using same output size and zero padding. $$ \begin{bmatrix} 0 & 1 & 0\\ 0 & 1 & 0\\ 0 & 1 & 0 \end{bmatrix} \otimes \begin{bmatrix} 1 & 2 & 1\\ 2 & 4 & 2\\ 1 & 2 & 1 \end{bmatrix} $$
(2) Perform the same convolution as above, but use repeat padding.
(3) Perform the same convolution as above, but use valid output size.
(4) Describe in words the result of applying the following filter using cross-correlation. If you aren't sure, try applying it to the image above to gain intuition.
$$ \begin{bmatrix} 0 & 0 & 0\\ 0 & 0 & 1\\ 0 & 0 & 0 \end{bmatrix} $$Let's mess with filter weights to do weird stuff.
h = np.array([
[0, 0, 0, 0, 0],
[0, 0, 0, 0, 0],
[1, 1, 1, 1, 1],
[0, 0, 0, 0, 0],
[0, 0, 0, 0, 0]],dtype=np.float64).T / 5
plt.imshow(filtering.filter(bg, h), cmap="gray")
<matplotlib.image.AxesImage at 0x7fe17da93e10>
h = np.array([
[1, 1, 1, 1, 1],
[1, -1, -1, -1, 1],
[1, -1, -1, -1, 1],
[1, -1, -1, -1, 1],
[1, 1, 1, 1, 1]], dtype=np.float64)
plt.imshow(filtering.filter(bg, h), cmap="gray")
plt.colorbar()
<matplotlib.colorbar.Colorbar at 0x7fe17daedb90>
Discrete cross-correlation:
$$ (f \otimes g)(x, y) = \sum_{j=-\ell}^\ell \sum_{k=-\ell}^\ell f(x+j, y+k) * g(j, k) $$Note that $g$ is defined with (0, 0) at the center.
Turns out there's a continuous version of this too! Sums become integrals:
$$ (f \otimes g)(x, y) = \int_{j=-\infty}^\infty \int_{k=-\infty}^\infty f(x+j, y+k) * g(j, k) $$Why $\infty$? Assume zero outside the boundaries.
Convolution vs cross-correlation
Properties
Aside: The filter above (with just a 1 in the middle) is called the identity filter.
A small modification to cross-correlation yields Convolution:
Cross-correlation ($\otimes$): $$ (f \otimes g)(x, y) = \sum_{j=-\ell}^\ell \sum_{k=-\ell}^\ell f(x+j, y+k) * g(j, k) $$ Convolution ($*$): $$ (f * g)(x, y) = \sum_{j=-\ell}^\ell \sum_{k=-\ell}^\ell f(x-j, y-k) * g(j, k) $$
This effectively flips the filter horizontally and vertically before applying it, and gains us commutativity.
orig = bg
blurred = filtering.filter(bg, g)
lost = orig - blurred
plt.imshow(orig, cmap="gray")
<matplotlib.image.AxesImage at 0x7fe17d981510>
plt.imshow(blurred, cmap="gray")
<matplotlib.image.AxesImage at 0x7fe17d852e50>
plt.imshow(lost, cmap="gray")
plt.colorbar()
<matplotlib.colorbar.Colorbar at 0x7fe17d7fdb90>
What if we add back what's lost?
plt.imshow(np.hstack([orig, orig + lost]), cmap="gray")
<matplotlib.image.AxesImage at 0x7fe17d74bc10>
(whiteboard - equations here for posterity) \begin{align*} I' &= I + (I - (I * G))\\ &= (I + I) - (I * G))\\ &= (I * D) - (I * G)\\ &= I * (D - G)\\ \end{align*}
Visual intuition:
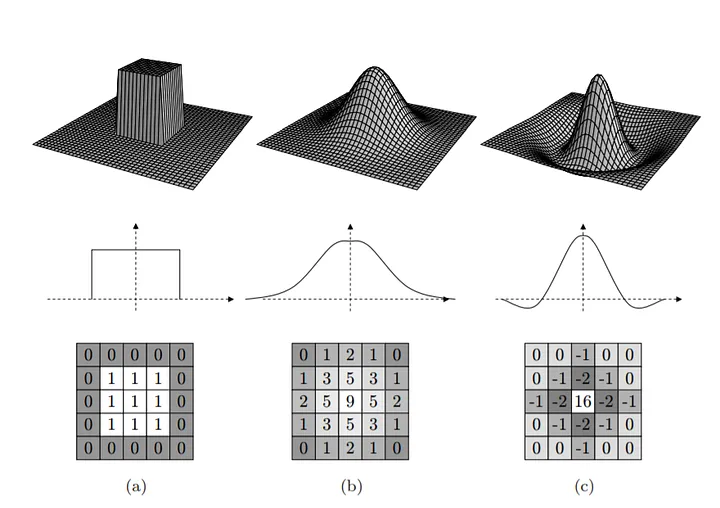
d = np.zeros_like(g)
d[4, 4] = 2
sharp = d - g
sharpened = filtering.filter(bg, sharp)
plt.imshow(np.hstack([orig, sharpened]), cmap="gray")
<matplotlib.image.AxesImage at 0x7fe17d749510>
Homework Problems 9-10:
Compute a 3x3 filter by convolving the following $1 \times 3$ filter with its transpose using full output size and zero padding: $$ \begin{bmatrix} 1 & 2 & 1\\ \end{bmatrix} $$
Suppose you have an image $F$ and you want to apply a $3 \times 3$ filter $H$ like the one above that can be written as $H = G * G^T$, where $G$ is $1 \times 3$. Which of the following will be more efficient?
Homework Problem 11:
(11) For each of the following, decide whether it's possible to design a convolution filter that performs the given operation.
Threshold: the output pixel is