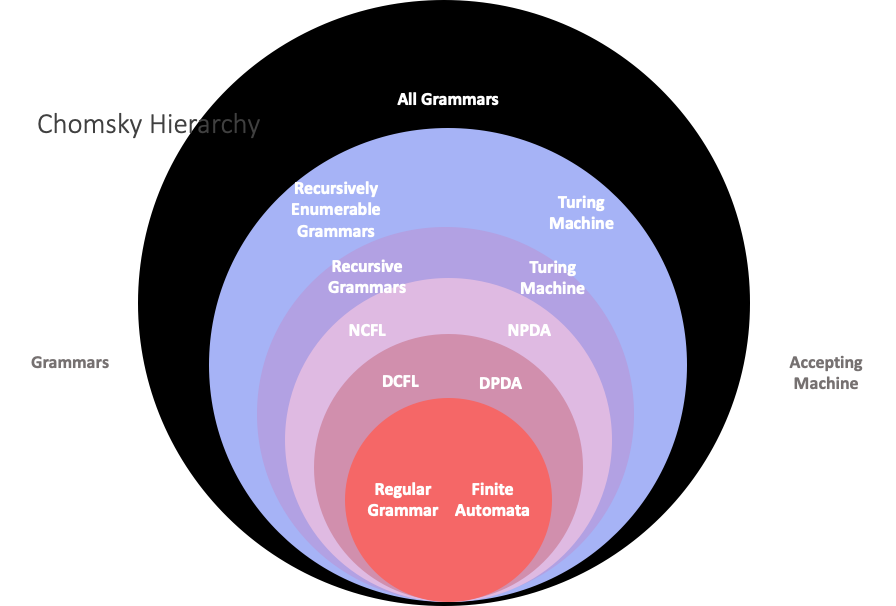
Here’s a prettier picture of the Chomsky Hierarchy (credit to Logan Sizemore):

Recall from way back when we introduced computability that we discussed the Halting Problem. In that lecture, I phrased it in terms of “programs”: Can you write a program that tells whether any given terminates? Thanks to the Church-Turing Thesis, we can equivalently rephrase this as: Can you design a Turing Machine that tells whether a given Turing Machine terminates on a given input?
Here’s the argument we used to show that such a program (or machine) cannot exist:
An alternative - and more general - way to prove that a problem is not decidable is to reduce its solution to the solution of a different problem that’s known to be undecidable. This is a very common tool employed in both computability theory and complexity theory - you’ll see this again!
Let’s look at an example. We will give a more rigorous proof that \(A_{TM}\) is not decidable by reducing HALT to \(A_{TM}\).
The general idea here is to demonstrate that if we could solve \(A_{TM}\), then we could solve HALT. Since we’ve already demonstrated that HALT is not decidable, this is sufficient to prove that \(A_{TM}\) is not decidable.
Theorem: \(A_{TM}\) is not decidable.
Proof: Suppose \(A_{TM}\) is decidable; that is, there exists a Turing machine \(M_{TM}\) that takes as input a TM and a string \(\langle M, w \rangle\) and accepts if \(M\) accepts \(w\) and rejects if \(M\) does not accept \(w\); in particular, \(M_{TM}\) always terminates, even if \(M\) does not.
Construct a Turing machine \(M_H\) that takes a machine and string \(\langle M, x \rangle\) as input. \(M_H\) operates as follows:
Observe that \(M_H\) is a solution to HALT that always terminates. Since HALT is undecidable, no such solution can exist; this is a contradiction, so our assumption that \(A_{TM}\) is decidable must be incorrect. \(\blacksquare\)
The above proof reduced HALT to \(A_{TM}\) to show that the latter is not decidable. You can also apply reductions to show that something is decidable. Whereas above we said “if (thing in question) were decidable, we’d be able to solve (undecidable problem)”. We can use similar reasoning to say “we can solve (thing in question) as long as we’re able to solve (decidable problems)”. We did this, informally, when showing that \(A_{NFA}\) is decidable: we argued that we can use \(M_{DFA}\) to solve \(A_{NFA}\) by first converting the NFA to a DFA (a process that will always terminate) then running \(A_{DFA}\) (which we know to be decidable). In this case, we reduced \(A_{NFA}\) to \(A_{DFA}\).
Rice’s theorem says that determining any nontrivial semantic property of a Turing machine is undecidable. Yikes!
Even among undecidable problems, there is a further distinction to be made: A language is enumerable (sometimes called recursively enumerable, or semi-decidable) if there exists a Turing machine that can generate all strings in the language. We may be able to do this even if we can’t fully solve the decision problem: equivalently, a language is enumerable if there is a turing machine that will accept all strings in the language in finite time (but may not reject all other strings in finite time).
Example: The set of halting turing machines