CSCI 301 L22 Worksheet

Lecture 22 - Exercises

Part A - NFA-DFA Conversion

In these exercises, we will convert the following NFA to a DFA:

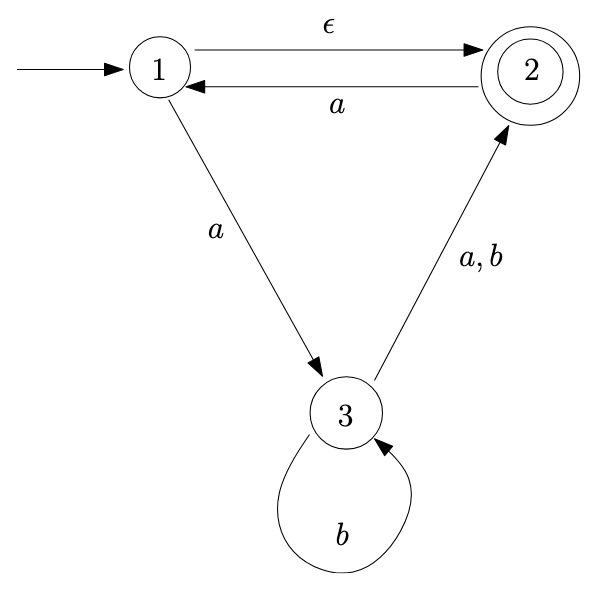
The \(\epsilon\)-closures of the states are as follows:

• \(C_\epsilon(1) = \{1, 2\}\)
• \(C_\epsilon(2) = \{1\}\)
• \(C_\epsilon(3) = \{2\}\)

1. Complete the state transition table of the equivalent DFA, including only reachable states:

2. Which of the states in the DFA are accept states?
3. Draw a diagram of the converted DFA.

Part B - Closure Proof Sketch

1. Given two DFAs \(M_A\) and \(M_B\) accepting languages \(A\) and \(B\), respectively, describe how to construct an NFA \(N\) for which \(L(N) = AB\).
2. Given a DFA \(M_A\) accepting language \(A\), describe how to construct an NFA \(N\) for which \(L(N) = A^*\).
3. Given a DFA \(M_A\), accepting language \(A\), describe how to construct an NFA \(N\) for which \(L(N) = \overline{A}\).
4. Given two DFAs \(M_A\) and \(M_B\) accepting languages \(A\) and \(B\), respectively, describe how to construct an NFA \(N\) for which \(L(N) = A \cap B\).

Part C - Regular Expressions

1. What language over \(\Sigma = \{a, b\}\) does each of the following regular expressions represent?

   1. \(ab\)
   2. \((a \cup b \cup \epsilon)\)
   3. \((ab \cup a)b\)
   4. \(a(a \cup b) \cup b(b \cup a)\)
   5. \(ab^*\)
   6. \((aa)^*\)
   7. \((ab)^* \cup b^*\)
   8. \((a^*b^*)^*\)

2. Write a regular expression that describes each of the following languages over \(\Sigma = \{0, 1\}\):

   1. \(\{w : w \text{ contains at least three $1$'s}\}\)
   2. \(\{w : |w| \text{ is odd}\}\)
   3. \(\{w : \text{ every odd position in $w$ is $1$}\}\)

3. Give a regular expression that describes the language accepted by the following DFA: