Lecture 21 - Exercises
Part A - NFA Design
Draw a diagram for an NFA that accepts each of the following
languages over the alphabet \(\{a,
b\}\).
- \(L = \{a\}\)
- \(L = \{w : w \text{ ends with }
ab\}\)
- \(L = \{w : w \text{ contains an odd
number of $a$'s or exactly two $b$'s}\}\)
Part B - NFA-DFA Conversion
Warmup
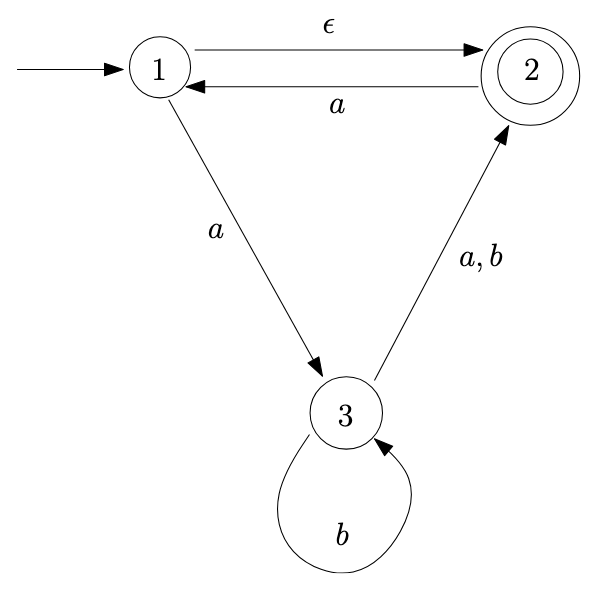
- Consider the NFA below. Ignoring \(\epsilon\) transitions, in which states
could the machine be in after processing the string \(aaa\)?
- Same question, but now allow for \(\epsilon\) transitions.

Part C - NFA-DFA Conversion
The \(\epsilon\)-closures of the
states are as follows:
- \(C_\epsilon(1) = \{1, 2\}\)
- \(C_\epsilon(2) = \{1\}\)
- \(C_\epsilon(3) = \{2\}\)
- Complete the state transition table of the equivalent DFA, including
only reachable states:
| Start |
\(\{1, 2\}\) |
\(\{1, 2, 3\}\) |
\(\varnothing\) |
|
\(\{1, 2, 3\}\) |
\(\{1,2,3\}\) |
\(\{2, 3\}\) |
|
|
|
|
|
|
|
|
- Which of the states in the DFA are accept states?
- Draw a diagram of the converted DFA.
Consider the following NFA:
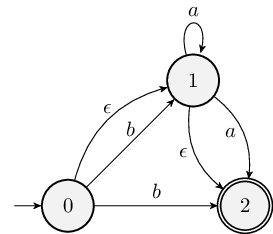
- Write its state transition table. This should have four columns:
State, \(a\), \(b\), and \(\epsilon\).
- Give the \(\epsilon\)-closure of
each state:
- \(C_\epsilon(0) =\)
- \(C_\epsilon(1) =\)
- \(C_\epsilon(2) =\)
- Construct the transition table for the equivalent DFA; this table
should have three columns: State, \(a\), and \(b\). You do not need to include unreachable
states.




