Lecture 18 - Exercises
Part A - Alphabets,
Strings, Languages
Let \(\Sigma = \{0, 1\}\) and \(A = \{a, b\}\) be two alphabets.
- \(1 \in \Sigma^*\)
- \(10 \in \Sigma^*\)
- \(\{1\} \in \Sigma^*\)
- \(\{1\}\) is a language over \(\Sigma\)
- \(\epsilon \in \Sigma\)
- \(\epsilon \in \Sigma^*\)
- \(101 \in (\Sigma \cup A)^*\)
- \(10ab \in (\Sigma \cup A)^*\)
- \(b \in (\Sigma - A)^*\)
Let \(S = \{\epsilon, 0, 1, 01, 11, 001,
011, 101, 111, \ldots\}\).
- Is \(S\) a language over \(\Sigma\)?
- Is \(S\) a language over \(A\)?
- Is \(S\) a language over \((\Sigma \cup A\))?
Part B - The Language
Accepted by a FA
Consider again the following DFA over alphabet \(\Sigma = \{0,1\}\):
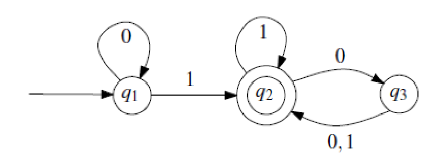
Which of the following strings are accepted by this machine?
\(1\)
\(00\)
\(001\)
\(10101\)
\(100\)
\(1000\)
Describe (informally, in English) the language accepted by this
machine.
Part C -
Deterministic vs Nondeterministic
For each of the following FAs, state whether it is a DFA.
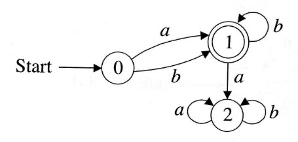
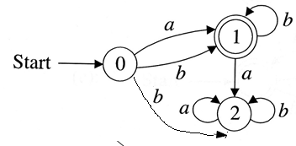
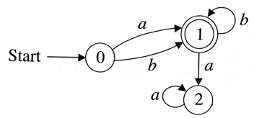
Part D - DFA Design
Draw a diagram for a DFA that accepts each of the following languages
over the alphabet \(\{a, b\}\).
- \(L = \{ab, abab, ababab,
\ldots\}\)
- \(L = \varnothing\)
- \(L = \{\epsilon\}\)
Draw a diagram for a DFA for each of the following languages over
\(\Sigma = \{0, 1\}\):
- \(L = \{w : |w| \text{ is divisible by
3}\}\)
- \(L = \{w : w \text{ as a binary number is
divisible by 4}\}\)




