Conjecture: The sum of the first \(n\) odd natural numbers is \(n^2\). In other words: \[ \sum_{i=1}^{n} 2n-1 = n^2 \] Is this true? It checks out for the first few values of \(n\):
\(1 = 1^2\)
\(1 + 3 = 2^2\)
\(1 + 3 + 5 = 3^2\)
But is it always true? What we’re trying to prove is an infinite sequence of statements \(S_i\), where
\(S_0: 1 = 1^2\)
\(S_1: 1 + 3 = 2^2\)
\(S_2 : 1 + 3 + 5 = 3^2\)
…and so on, including \(S_k\) for any \(k \in \mathbb{N}\).
Induction is recursion’s mathematical sibling. Here’s an argument:
\(S_0\) is true because \(1 = 1^2\).
Suppose \(S_k\) is true, meaning that \(1 + 3 + \ldots + 2k-1 = k^2\). Add \(2k + 1\) to both sides, yielding \[ 1 + 3 + \ldots + (2k-1) + (2k+1) = k^2 + 2k + 1 \] Factoring the right-hand side, we have
\[ 1 + 3 + \ldots + (2k-1) + (2k+1) = (k + 1)^2 \] Therefore, the sum of the first \(k+1\) odd numbers is equal to \((k+1)^2\).
We have shown that if \(S_k\) is true, then \(S_{k+1}\) is true. \(\blacksquare\)
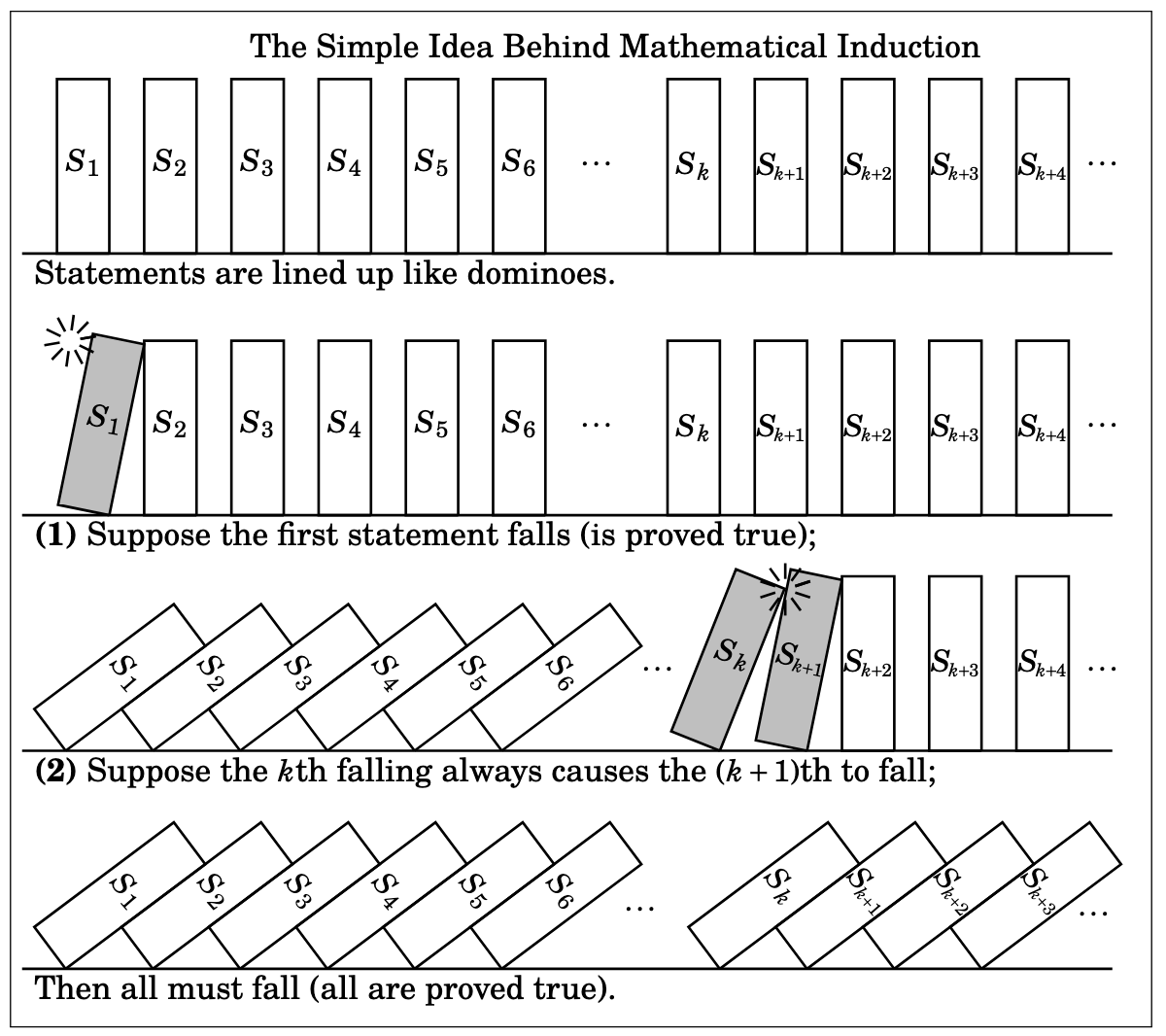
An analogy for why this makes sense is dominoes: if you’ve lined them all up so each one knocks the next one over, all you need to knock them all over is to knock over the first one:

\(S_0\) is true, because \(1 = 1^2\).
This is called the base case. It’s analogous to the base case in a recursive function or definition. This is showing that “the first domino falls”.
Suppose \(S_k\) is true
This is called the inductive hypothesis. This is saying “if we knock the \(k\)th domino over…”
At this point, all we need is to show that \(S_k \Rightarrow S_{k+1}\); in doing so, we complete the inductive step, or the inductive case. To do this is to complete the above sentence with “… then the \(k+1\)th domino falls as well.”
Spend some time attempting Ex. A #1
Proposition: \(3 \mid (5^{2n} -1)\) for every integer \(n \ge 0\).
Proof: We prove this by induction.
(Base case): Observe that \(3 \mid 5^{(2\cdot0)} - 1 = 0\), so the proposition is true for \(n = 0\).
(Inductive case): Suppose that \(3 \mid (5^{2k} - 1)\) for some \(k \ge 0\). We now need to show that \(3 \mid (5^{2(k+1)} - 1)\).
Because \(3 \mid (5^{2k} - 1)\), we know that \(5^{2k} - 1 = 3c\) for some integer \(c\). We can multiply both sides by \(5^2\), giving: \[ \begin{align*} 5^2 \cdot 5^{2k} - 1 &= 3c \cdot 5^2\\ 5^{2k + 2} &= 3(25c)\\ 5^{2(k + 1)} &= 3(25c) \end{align*} \] The right-hand side implies that the left-hand side is divisible by 3, so we have showed that if \(3 \mid (5^{2k} - 1)\), then \(3 \mid (5^{2(k+1)} - 1)\), completing the proof by induction. \(\blacksquare\)
Do Exercises Part A
Do Exercises Part B, as time allows