CSCI 301 L04 Notes

Lecture 4 - Notes

Logic 1

determine whether an English sentence or a mathematical expression is a logical statement.
articulate the meanings of and know the truth table for logical AND, OR, NOT, operators
articulate the meaning of and know the truth table for the conditional operator

Announcements

A1
- Reminder: due Friday. We covered everything you need as of yesterday.
- Reminder: you must submit a PDF generated by LaTeX from the provided .tex template. See the guide and come to office hours if you’re having trouble.
Lab 1 is due Sunday night
Siddhu’s office hours are posted - Thursday 12-12:30; Arun’s still TBD
- You can go to either TA’s office hours for help, regardless of whether they’re your lab TA

Statements

Definition: A statement is an English sentence or mathematical expression that is either definitely true or definitely false. That is, a statement has a definite truth value (true or false).

Examples:

Sentence/Expression	Statement?
Add \(5\) to both sides	No
\(\mathbb{Z}\)	No
Adding \(5\) to both sides of \(x-5=37\) gives \(x=42\)	Yes
\(42 \in \mathbb{Z}\)	Yes
\(42\)	No
What is the solution of \(2x=84\)?	No
The solution of \(2x=84\) is \(41\)	Yes
\(42\) is not a number	Yes
\(x\) is a multiple of \(8\)	No

This last one,

\(x\) is a multiple of \(8\)

has a truth value that depends on the value of \(x\). Thus - by itself - it’s not definitely true or false, and is not a statement. But if you give me a value for \(x\), it becomes a statement because that value is either a multiple of 8 or it is not. This is an example of…

Definition: an open sentence is a sentence or expression that is not a statement because its truth value depends on one or more variables.

Aside: There can be statements we don’t know the truth value of…

…but they still have one.

A sentence can be a statement even if we mortal humans don’t know which!

Nonexample:

it is not cloudy

This isn’t a statement because its truth value depends (for example) on where in the world you are - there is no secret unknown “true” value of whether it is cloudy - it is not definitively true or false. To make it a statement, you’d need to say something more specific.

Example: The Collatz Conjecture

Start with a positive integer \(x\). Repeat the following:

if \(x\) is even, divide it by 2 (\(x \leftarrow x / 2\))

if \(x\) is odd, multiply \(x\) by 3 and add 1 (\(x \leftarrow 3x + 1\))

Given any initial positive integer \(x\), after iterating this a finite number of times, \(x\) becomes 1.

This is a statement (it’s either true or not). But nobody has figured out which!

Do Exercises Part A

Logical Operators (and, or, not)

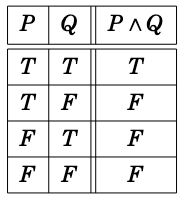
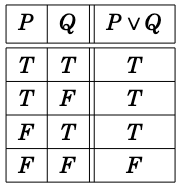
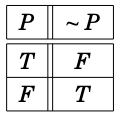
Three important logical operators that operate on statements:

and: \(P \land Q\) is true if both \(P\) and \(Q\) are true, and is false otherwise
or: \(P \lor Q\) is true if at least one of \(P\) and \(Q\) is true, and is false otherwise
not: \(\neg P\) (also sometimes written \(\sim P\) ) is true if \(P\) is false, and false if \(P\) is true

The following show truth tables, where the last column is the value of the expression for the given value(s) of the input(s) in the left column(s).

Do Exercises Part B

Conditional Statements

Here’s the truth table for the conditional operator:

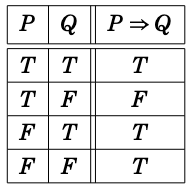
The usual interpretation of \(P \Rightarrow Q\) is to mean “if \(P\) then \(Q\)”, or “\(P\) implies \(Q\)”

Notice: this does not commute.

\(P\) : \(x = y\)
\(Q\) : \(x^2 = y^2\)
\(R\) : If \(P\) then \(Q\) (a true statement)
\(S\) : If \(Q\) then \(P\) (a false statement)

False Implies Anything Weirdness

Notice: If false, then anything! This gets weird sometimes.

\(P\) : If I am healthy, then I will come to class.

Suppose you are sick; then the statement “If I am healthy, then I will come to class” is true whether or not you come to class.

Mental model suggestions:

Apply the truth table and don’t think too hard
Think of \(P \Rightarrow Q\) as a promise that anytime \(P\) is true, \(Q\) will also be true; but it doesn’t promise any more than that.
The first 2 rows are the ones we’ll actually be using.

Do Exercises Part C

Natural Language Weirdness

Equivalent ways of writing “if \(P\) then \(Q\)”:

If \(P\), then \(Q\)
\(Q\) if \(P\)
\(Q\) whenever \(P\)
Whenever \(P\), then also \(Q\).
\(P\) is a sufficient condition for \(Q\).
\(Q\) is a necessary condition for \(P\).
\(Q\) only if \(P\).

Definition/aside: “If \(Q\) then \(P\)” is the converse of “If \(P\) then \(Q\)”.

Do Exercises Part D

Biconditional Statements

Biconditional - “\(P\) if and only if \(Q\)”: \(P \Leftrightarrow Q\)

This means \(P \Rightarrow Q\) and \(Q \Rightarrow P\) are both true.