CSCI 301 L03 Notes

Lecture 3 - Notes

Outcomes

Sets 2

• Know the definition of subset, power set.
• Compute a Cartesian Product of two or more sets.
• Understand the notation and meaning for: union, intersection, difference, and complement
• Be able to draw and interpret Venn diagrams

Announcements

• Office hours are finalized and posted:
  • Tuesday 12-1
  • Wednesday 2-3
  • Friday 1-2

Subsets and Powersets

Definition: Suppose \(A\) and \(B\) are sets. If every element of \(A\) is also an element of \(B\), then \(A\) is a subset of \(B\); this is denoted \(A \subseteq B\).

For example, let:

• \(A = \{1, 2, 3\}\)
• \(B = \{2, 3, 1\}\)
• \(C = \{1, 2\}\)

Then the following are true:

1. \(A \subseteq B\)
2. \(B \subseteq A\)
3. \(C \subseteq A\)
4. \(C \not\in A\)
5. \(A \not\subseteq C\)
6. \(\{n^2 : n \in \mathbb{Z}\} \subseteq \mathbb{Z}\)

Aside: If \(A \subseteq B\) and \(A \ne B\), then \(A\) is a proper subset of \(B\), denoted \(A \subset B\).

• Examples, using the sets above:
  • \(A \not\subset B\)
  • \(C \subset A\)
  • \(\{n^2 : n \in \mathbb{Z}\} \subset \mathbb{Z}\)

Definition: The power set of a set \(A\) is the set of all subsets of \(A\). It is denoted \(\mathcal{P}(A)\), or sometimes \(2^A\). In other words, \(\mathcal{P}(A) = \{S : S \subseteq A\}\).

Do Exercises Part A

Cartesian Product

Terminology/notation:

• An ordered pair (sometimes called a 2-tuple, or just a pair) is usually written \((a, b)\). This is an object with a first and second element (i.e., order matters)
• A tuple generalizes this to more than just two items; \((a, 4, 4)\) would be called a 3-tuple.
• Key observations: unlike sets, order matters and items are not necessarily unique.

Definition: The Cartesian product of two sets \(A\) and \(B\), denoted \(A \times B\), is the set of ordered pairs \((a, b)\) where \(a \in A\) and \(b \in B\). \[ A \times B = \{\left(a, b\right) : a \in A \text{ and } b \in B\} \] Example: \[ \begin{align*} A &= \{a, b\}\\ B &= \{1, 2, 3\} \end{align*} \]

\[ A \times B = \{(a, 1), (a, 2), (a, 3), (b, 1), (b, 2), (b, 3)\} \]

Generalization: The cartesian product generalizes to any number of sets: \(A \times B \times C\) is the set of all ordered triples (or 3-tuples) whose members are from \(A\), \(B\), and \(C\) respectively.

Do Exercises Part B

Set Operations

Definitions:

• The union of two sets \(A \cup B\) is the set \(\{x : x \in A \text{ or } x \in B\}\)
• The intersection of two sets \(A \cap B\) is the set \(\{x : x \in A \text{ and } x \in B\}\)
• The difference of two sets \(A - B\) is the set \(\{x : x \in A \text{ and } x \notin B\}\). It’s also sometimes written \(A \setminus B\).

Example: Let \(S = \{1, 2, 3\}\) and \(T = \{2, 4\}\).

• \(S \cup T = \{1, 2, 3, 4\}\)
• \(S \cap T = \{2\}\)
• \(S - T = \{1, 3\}\)
• \(T - S = \{4\}\)

Do Exercises Part C

Complement, Venn diagrams

When talking about a set \(P\), it’s often useful to talk about it in terms of a universal set \(U\), where \(P \subseteq U\), where \(U\) is (informally) the set of all things that might have been considered for membership in \(P\). Notice that this is informal and context-dependent, but useful nonetheless:

• If talking about the set of prime numbers, then \(\mathbb{N}\) makes for a natural universal set.

• If talking about odd numbers, then \(\mathbb{Z}\) makes for a natural universal set.

• If talking about the set of students enrolled in this class, the universal set might be all CS premajors, or all students taking classes in CSE departments, all Western students, or all university students in the USA.

Definition If \(A\) has a universal set \(U\), then the complement of \(A\), denoted \(\overline{A}\), is the set \(\overline{A} = U - A\).

Examples:

• If \(E\) is the set of even numbers with universal set \(\mathbb{Z}\), then \(\overline{E}\) is the set of odd numbers.

• In our Exercises Part C, we can consider \(U\) to be the universal set for \(A\) and \(B\), so \(\overline{A} = \{2, 4, 6, \ldots, 20\}\).

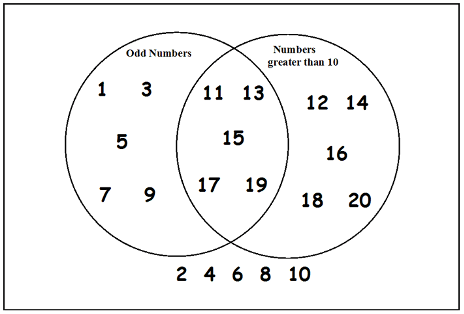
Venn Diagrams are a useful way to visualize sets and their relations with each other:

Here,

Let \(U\) = \(\{x : x \in \mathbb{N} \text{ and } x \le 20\}\) is the contents of the rectangular box.

Let \(A = \{x : x \in U \text{ and } x \text{ is odd}\}\) is the contents of the left circle.

Let \(B = \{x : x \in U \text{ and } x > 10\}\) is the contents of the right circle.

\(A \cup B\) is the contents of both circles.

\(A \cap B\) is the contents of the region where the circles overlap.

Do Exercises Part D