CSCI 301 L32 Notes

Lecture 32 - Notes

Goals

Be able to prove that a language is not regular using the Pumping Lemma for Regular Languages
Be able to prove that a langauge is not context-free using the Pumping Lemma for Context-Free Languages

Announcements

Lab 8 is out, so you can start if you’d like; I made some edits to the writeup and fixed one documentation bug in the skeleton code on Sunday morning.
- If you downloaded the skeleton before Sunday: The parse table entry for the L production with $ as the lookahead symbol should be e (epsilon), not err (error).
A8 is due Wednesday; Week 8 Survey due Wednesday

Classifying Languages

At this point, we have encountered two major classes of languages: regular and context-free. We’ve stated, but not proved, that all regular languages are context-free. We’ve seen a few examples of languages that are context-free but not regular, such as $a^nb^n$.

But how, in general, can we prove that a language is not in a given class? If we can find a DFA it’s regular, but how can we prove that no DFA can possibly exist? The answer to this question is called the Pumping Lemma.

The Pumping Lemma for Regular Languages

The intuition is simply that, for a DFA to exist for an infinite language, there has to be some kind of repetitive structure that allows the DFA to recognize infinite strings using only a finite number of states.

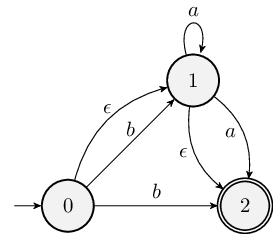
Considering the following NFA: what can say for sure about a string accepted by this machine if the string’s length is greater than 2?

Notice that the only way for an accepted string to be longer than 2 characters is to spend some time in State 1, repeating $a$’s. In other words, any string longer than 2 characters must have the form $(\epsilon \cup b)a^*(\epsilon\cup a)$. Considering the three parts of this regular expression, the key observation is that the middle part must be something with a star, and such a middle part must always exist for any FA that accepts an infinite language.

With finite states, there must be some string length, beyond which any accepted string must take one or more trips through a path that begins and ends at the same state.

The pumping lemma formalizes this as follows:

Lemma (The Pumping Lemma for Regular Languages): Let $A$ be a regular language. Then there exists an integer $p \ge 1$, called the pumping length, such that the following holds: Every string $s$ in $A$ with $|s| \ge P$ can be written as $s = xyz$, where

$y \ne \epsilon$ (i.e., $|y| \ge 1$)
$|xy| \le p$, and
for all $i \ge 0$, $xy^iz \in A$.

Here’s a picture that summarizes the pumping lemma:

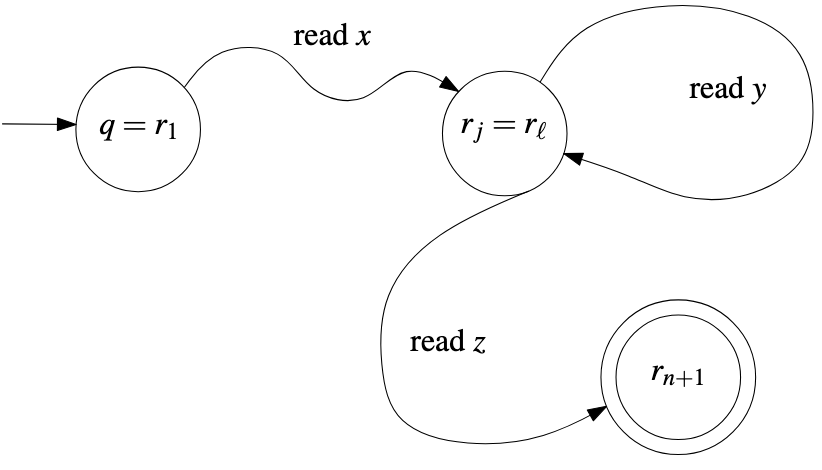
pumping

Proof: Suppose $A$ is regular; then there exists a DFA $M = (Q, \Sigma, \delta, q, F)$ that accepts it. Let $p$ be the number of states in $Q$. Consider a string $s = s_1 s_2 s_3 \ldots s_n$ be a string in $A$ with $n \ge p$, and let the states $r_1, r_2, r_3, \ldots, r_{n+1}$ be the states visited while processing $s$, where $r_1 = q$ and the machine switches to state $r_{i+1}$ after processing character $s_i$.

Since the number of states in $M$ is $p$ and the number of states visited while processing $s$ is $n+1$, the states $r_i$ cannot all be distinct, or in other words, some state is visited twice. In fact, a state must be repeated by the time state $r_{p+1}$ has been visited, because at this point $|Q|+1$ states have been visited. Let $j$ and $\ell$ be the indices in the state transition list of a repeated state (i.e., $r_j = r_\ell$), with $j < \ell$. Observe taht $1 \le j < \ell \le p+1$. Now we can define:

$x = s_1 s_2 \ldots s_{j-1}$
$y = s_j \ldots s_{\ell-1}$
$z = s_{\ell} \ldots s_n$

This satisifes the properties given in the pumping lemma:

Since $j < \ell$, we have that $|y| \ge 1$.
Taking $|xy|$ steps from $r_1$ leaves the machine in state $r_{\ell = |xy|+1}$. Since $\ell \le p+1$, this means $|xy| +1 \le p + 1$, or $|xy| \le p$.
Since $xyz$ is accepted by $M$, the machine reads $x$ to get to $r_j$, then reads $y$ and returns to $r_j = r_\ell$, then reads $z$ to reach the final accept state $r_{n+1}$. Notice that starting at state $r_j$ and reading $y$ takes a particular journey through the machine that returns the machine to $r_j$. Given the string $xz$, the machine would skip that journey and still reach the same final state. Similarly, it could make the journey two or more times by reading $xyyz$, $xyyyz$, and so on. $\blacksquare$

Proving Languages are Not Regular

The pumping lemma states something about regular languages; to prove something is not regular, we will use proof by contradiction by supposing the lemma holds, then showing a contradiction.

Example Prove that $A = \{0^n 1^n : n \ge 0\}$ is not regular.

Proof: We will prove this by contradiction. Assume that $A$ is regular, and let $p \ge 1$ be the pumping length given by the pumping lemma. Consider the string $s = 0^p 1^p$. The conditions of the pumping lemma are satisfied: $s \in A$ and $|s| = 2p \ge p$. Thus by the pumping lemma, $s$ can be written as $s = xyz$ where $y \ne \epsilon$, $|xy| < p$, and $xy^iz \in A$ for any $i \ge 0$.

Because $s = 0^p 1^p$ and $|xy| \le p$, notice that $xy$ must be made up of all zeros, and $y$ is not empty so it has at least one zero. If we let $|y| = k$, then $xz = 0^{p-k}1^p$. However, by the pumping lemma, $xz \in A$, which is a contradiction, so $A$ cannot be regular.

Strategy Note

In general, the “trick” to pumping lemma proofs is to pick the right string $s$ given the pumping length $p$. In the above proof, we picked $0^p1^p$ because that makes $xy$ all zeros, and from there we can only add or subtract zeros by subbing $y^i$.

(End of what we covered in L32)

The Pumping Lemma for Context-Free Languages

There is an equivalent lemma that can be used to show that a language is not context-free. The intuition is similar, except instead of “looping” journies through a state machine, we observe that subtrees of the parse tree must be repeated. We won’t cover this in much detail, but here’s the lemma:

Lemma (The Pumping Lemma for Context-Free Languages): Let $L$ be a context-free language. Then there exists an integer $p \ge 1$, called the pumping length, such that every string $s$ in $L$ with $|s| \ge p$ can be written as $s = uvxyz$, where

$|vy| \ge 1$ (i.e., $v$ and $y$ are not both empty)
$|vxy| \le p$, and
$uv^ixy^iz \in L$ for all $i \ge 0$.

This can be used to prove, for example, that $A = \{a^nb^nc^n : n \ge 0\}$ is not context-free.

Proof Sketch: Consider the string $a^p b^p c^p$, and looks quite similar to the $a^nb^n$ regular proof, except that we have to address three cases for the location of $vxy$. Since $u$ and/or $w$ could be empty, we consider three cases:

$vxy$ doesn’t have any $c$; that is, it’s entirely in the $a^pb^p$ part.
- In this case, $uv^2xy^2z$ adds $a$’s or $b$’s but not $c$’s.
$vxy$ doesn’t have any $a$; that is, it’s entirely in the $b^pc^p$ part.
- A symmetric argument can be made, pumping can add only $b$’s or $c$’s.
$vxy$ cannot contain $a$’s, $b$’s, and $c$’s,’ because its length is less than or equal to $p$

Thus there’s no way to break $s$ into $uvxyz$ that satisfies the CF pumping lemma criteria, so the language cannot be context-free.