CSCI 301 L27 Notes

Lecture 27 - Notes

Goals

Know the definition of a context-free grammar.
Know how to apply grammar rules to derive a string in a grammar’s language
Know the definition of leftmost and rightmost derivation
Know how to determine whether a grammar is ambiguous

Announcements

Racket tip:
There are a couple ways to “fake” imperative style (that is, “do this then do that”) in Racket:
```
(begin
  (do this)
  (do that))
```
or
```
(let (bindings here) 
  (do this)
  (do that))
```
Midterm wrapper due tonight

Context-Free Languages

Today, we climb one level up the Chomsky Hierarchy to the next class of languages: context-free languages. Whereas:

regular languages can be described by regular expressions and accepted by finite automata,
context-free languages are described by context-free grammars and accepted by pushdown automata.

Context-Free Grammars

We’ll start by describing context-free languages with grammars, and later we’ll see the machines that accept them.

Example: The following is a context-free grammar: \[ \begin{align*} S &\rightarrow AB \\ A &\rightarrow a\\ A &\rightarrow aA\\ B &\rightarrow b\\ B &\rightarrow bB\\ \end{align*} \] Each symbol in the grammar is either:

a variable, also known as a nonterminal, which belong to a set $V$. In the above grammar, $V = \{S, A, B\}$.
a terminal, which belong to an alphabet $\Sigma$. In the above grammar, $\Sigma = \{a, b\}$.

The grammar is composed of rules or productions. In this case, $S$ is a special variable called the start symbol. Strings in the language described by this grammar can be created by deriving them from the start symbol. Here’s an example: \[ \begin{align*} S &\Rightarrow AB \\ &\Rightarrow aAB &\text{ (using $A \rightarrow aA$) }\\ &\Rightarrow aAbB &\text{ (using $B \rightarrow bB$) }\\ &\Rightarrow aaAbB &\text{ (using $A \rightarrow aA$) }\\ &\Rightarrow aaaabB &\text{ (using $A \rightarrow a$) }\\ &\Rightarrow aaaabb &\text{ (using $B \rightarrow b$) }\\ \end{align*} \] Notice that the symbol $\rightarrow$ appears in the rules, whereas $\Rightarrow$ is used to denote the application of one of those rules to a particular string.

Definition: Let $A \in V$ be a nonterminal, and $u, v, w \in (\Sigma \cup V)^*$ be strings, and suppose $A \rightarrow w$ is a rule in the grammar. Then we say that $uwv$ can be derived in one step fron $uAv$; we write this $uAv \Rightarrow uwv$.

We can generalize this to the operator $\Rightarrow^*$, where $u \Rightarrow^* v$ means means $v$ can be derived from $u$ in zero or more steps.

Definition: A context-free grammar is a 4-tuple $(V, \Sigma, R, S)$, where

$V$ is the set of variables (nonterminals)
$\Sigma$ is the alphabet of terminals
$R$ is a finite set of rules of the form $A \rightarrow w$, with $A \in V$ and $w \in (V \cup \Sigma)^*$.
$S \in V$ is the start symbol or start variable.

Notice the important restriction that the left side of a rule must be a single nonterminal. This is what separates context-free from context-sensitive grammars.

Definition: The language of a grammar $G$ is the set of all strings in $\Sigma^*$ that can be derived (in any number of steps) from $S$: \[ L(G) = \{w \in \Sigma^* : S \Rightarrow^* w\} \] Definition: A language $A$ is context-free if there exists a context-free grammar $G$ such that $L(G) = A$.

Here’s a language that’s not regular but is context-free: \[ L = \{a^n b^n\} = \{\epsilon, ab, aabb, aaabbb, \ldots\} \] And here’s a grammar that generates it: \[ \begin{align*} S &\rightarrow \epsilon\\ S &\rightarrow aSb \end{align*} \] Here’s a derivation of $aaabbb$:

$S \Rightarrow aSb \Rightarrow aaSbb \Rightarrow aaaSbbb \Rightarrow aaabbb$

Note on notation: we can write rules with the same left-hand side with $\mid$, interpreted as “or”; the grammar above could be written: \[ S \rightarrow \epsilon \mid aSb. \] Sometimes we split these “or” productions onto multiple lines, as in \[ \begin{align*} B \rightarrow & b \\ \mid& bB \end{align*} \] though I haven’t yet found a great way to typeset this and have it look nice.

Parse Trees

Consider the grammar and derivation from above:

\[ \begin{align*} S &\rightarrow AB \\ A &\rightarrow a\\ A &\rightarrow aA\\ B &\rightarrow b\\ B &\rightarrow bB\\ \end{align*} \]

\[ \begin{align*} S &\Rightarrow AB \\ &\Rightarrow aAB &\text{ (using $A \rightarrow aA$) }\\ &\Rightarrow aAbB &\text{ (using $B \rightarrow bB$) }\\ &\Rightarrow aaAbB &\text{ (using $A \rightarrow aA$) }\\ &\Rightarrow aaaabB &\text{ (using $A \rightarrow a$) }\\ &\Rightarrow aaaabb &\text{ (using $B \rightarrow b$) }\\ \end{align*} \] We can represent this derivation using a parse tree, where each level of the tree is an intermediate string. Every time a rule is applied, the nonterminal being substituted branches into the characters that replace it.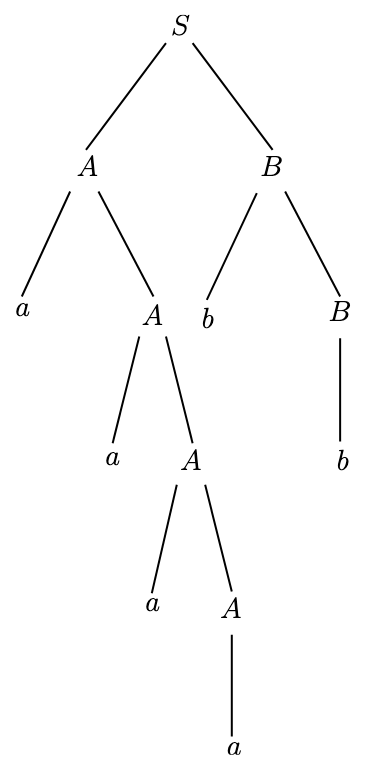

Leftmost, Rightmost Derivation

Consider the following grammar over the alphabet $\Sigma = \{0, 1, \ldots 9, +, -, *, /, (, )\}$: \[ \begin{align*} E &\rightarrow E + E \\ E &\rightarrow E - E\\ E &\rightarrow E * E\\ E &\rightarrow E / E\\ E &\rightarrow (E)\\ E &\rightarrow 0 \mid 1 \mid 2 \mid 3 \mid 4 \mid 5 \mid 6 \mid 7 \mid 8 \mid 9 \end{align*} \] Consider the string $1 + 1 * 4$. We can derive it in many ways! Three examples:

$E \Rightarrow E + E \Rightarrow E + E * E \Rightarrow 1 + E * E \Rightarrow 1 + E + 4 \Rightarrow 1 + 1 + 4$
$E \Rightarrow E + E \Rightarrow 1 + E \Rightarrow 1 + E * E \Rightarrow 1 + 1 * E \Rightarrow 1 + 1 * 4$
$E \Rightarrow E * E \Rightarrow E * 4 \Rightarrow E + E * 4 \Rightarrow E + 1 * 4 \Rightarrow 1 + 1 * 4$

These all get to the same string, but by a different route. Notice:

Derivation #2 is a left-most derivation, because a rule is always applied to the left-most nonterminal
Derivation #3 is a right-most derivation because a rule is always applied to the right-most nonterminal.

Ambiguous Grammars

If we construct the parse trees for the above derivations, we’ll notice that we can get different parse trees. Specifically #1 and #2 yield the same parse tree, where #3 has a different one. Knowing what we know about order of operations, we’d probably hope to get the parse tree from #1 in this case (but notice that using the left-most derivation doesn’t solve this universally - the situation would be reversed for $1 * 1 + 4$).

Definition: A grammar $G$ is ambiguous if there is some string $w \in L(G)$ with more than one distinct parse tree.

Equivalent definition: A grammar $G$ is ambiguous if there is some string $w \in L(G)$ that has more than one left-most derivation.