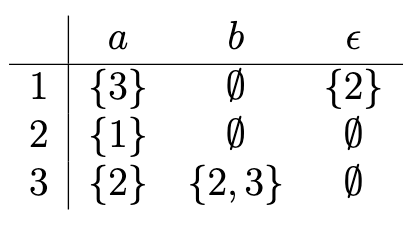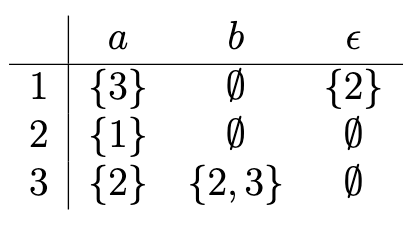CSCI 301 L25 Worksheet

Lecture 25 - Exercises

Part A - NFA-DFA Conversion Warmup

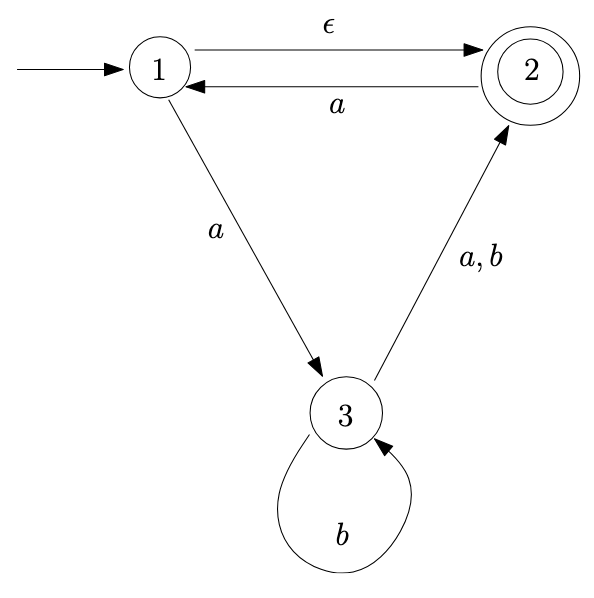
1. Consider the NFA below. Ignoring \(\epsilon\) transitions, in which states could the machine be in after processing the string \(aaa\)?
2. Same question, but now allow for \(\epsilon\) transitions.

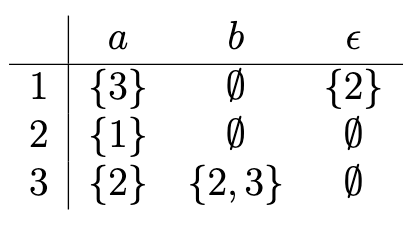
Part B - NFA-DFA Conversion

The \(\epsilon\)-closures of the states are as follows:

• \(C_\epsilon(0) = \{1, 2\}\)
• \(C_\epsilon(1) = \{1\}\)
• \(C_\epsilon(2) = \{2\}\)

1. Complete the state transition table of the equivalent DFA, including only reachable states:

2. Which of the states in the DFA are accept states?
3. Draw a diagram of the converted DFA.

Part C - Closure Proof Sketch

1. Given two DFAs \(M_A\) and \(M_B\) describe how to construct an NFA \(N\) for which \(L(N) = AB\).
2. Given a DFA \(M_A\), describe how to construct an NFA \(N\) for which \(L(N) = A^*\).
3. Given a DFA \(M_A\), describe how to construct an NFA \(N\) for which \(L(N) = \overline{A}\).
4. Given two DFAs \(M_A\) and \(M_B\) accepting languages \(A\) and \(B\), respectively, describe how to construct an NFA \(N\) for which \(L(N) = A \cap B\).

Part D - Extra Practice NFA-DFA Conversion

Consider the following NFA:

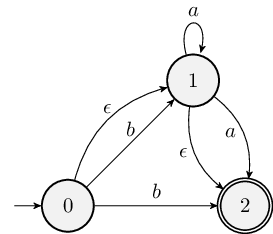
1. Write its state transition table. This should have four columns: State, \(a\), \(b\), and \(\epsilon\).
2. Give the \(\epsilon\)-closure of each state:
   1. \(C_\epsilon(0) =\)
   2. \(C_\epsilon(1) =\)
   3. \(C_\epsilon(2) =\)
3. Construct the transition table for the equivalent DFA; this table should have three columns: State, \(a\), and \(b\). You do not need to include unreachable states.