CSCI 301 L25 Notes

Lecture 25 - Notes

Goals

• Know how to convert a DFA to an NFA
• Be able to prove that regular languages are closed under regular operations including union, concatenation, and star.

Announcements

• I extended the A6 deadline to Friday. Still aiming to get A7 out tomorrowish.

The Regular Languages are closed under the regular operations

A Medium-Large Question

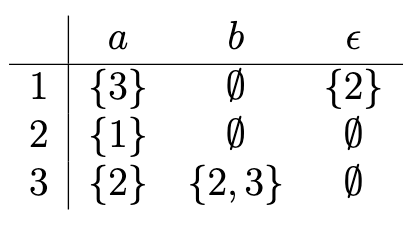
We’ve seen that the regular languages are those that have an accepting DFA.

Question: Are NFAs more powerful? In other words, are there languages that NFAs can accept that DFAs can’t?

If NFAs are no more powerful than DFAs, then things get a lot easier: for example, the following language from the Exercises is simply the union of two languages: \[ L = \{w : w \text{ contains an odd number of $a$'s or exactly two $b$'s}\} \]

and the approach that works to build an NFA from this (that is, joining each language’s DFA with an \(\epsilon\) transition from a shared start state) could work on any pair of languages!

It turns out that no, NFAs are not more powerful.

Converting an NFA to a DFA

Theorem: For any NFA \(N\), there exists an equivalent DFA \(M\) such that \(L(M) = L(N)\).

Proof: Suppose \(N\) is an NFA \((Q, \Sigma, \delta, q, F)\). We show how to construct a DFA \(M = (Q', \Sigma', \delta', q', F')\) such that \(L(M) = L(N)\).

Here we will not give the formal proof in its full generality, but work through an example and convince ourselves that this approach works in general. The game plan here is to design a DFA that runs all possible computations that the NFA could run on the input. The process is somewhat similar to how we proved the union case for DFAs, except instead of each DFA state corresponding to pairs of original machine states, they will represent sets of states that the input machine might have been in.

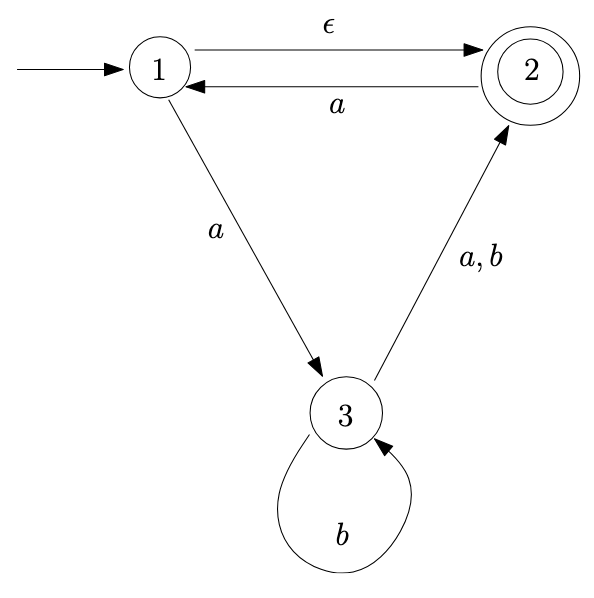
Consider the following NFA; for convenience, I’ve also included its transition table:

Do Exercises - Part A

See the whiteboard notes, and also Section 2.5 of TC. Section 2.5 gives the general process, while Section 2.5.1 shows the conversion for this example.

Do Exercises - Part B

Closure of Regular Languages under Regular Operations

We’re finally ready to do the (actually quite straightforward, now!) proof of the closure of regular operations.

Theorem: The set of regular languages is closed under the regular operations.

Regular Operations

• The union of two languages \(A\) and \(B\) is defined as \(A \cup B = \{w : w \in A \text{ or } w \in B\}\).
• The concatenation or product of two languages \(A\) and \(B\) is defined as \(AB = \{ww' : w \in A \text{ and } w' \in B\}\).
• The closure or star (or Kleene closure) of a language \(A\) is defined as: \(A^* = \{u_1 u_2 \ldots u_k : k \ge 0 \text{ and } u_i \in A \text{ for all } i = 1, 2, \ldots, k\}\)
  • In other words, it’s the language containing all possible concatenations of any choice of 0 or more strings over \(A\). Notice that 0 is an option here, so \(\epsilon \in A^*\) for any language \(A\).
  • Another equivalent recursive definition is:
    • Let \(A^0 = \{\epsilon\}\)
    • Let \(A^k = AA^{k-1}\)
    • \(A^* = \bigcup_{k=0}^{\infty} A^k\)

Proof:

• Case: \(A \cup B\) - see whiteboard notes for proof sketch.
• Remaining cases: Exercises!