CSCI 301 L23 Notes

Lecture 23 - Notes

Goals

• Be able to construct a DFA that accepts simple languages
• Know how to perform the following regular operations on languages:
  • Union
  • Concatenation
  • Closure (star)
• Know the definition and construction for regular languages, and know that they are closed under the union operation.

Announcements

• A5, Week 5 Survey due tonight

Cool demo: https://web.stanford.edu/class/archive/cs/cs103/cs103.1142/button-fsm/

The Language Accepted by a FA

Informally: a finite automata accepts a string if the automata can begin in the start state and process each symbol in the string and end in an accept state.

Formally:

Definition: Let \(M = (Q, \Sigma, \delta, q, F)\) be a finite automaton and let \(w = w_1 w_2 w_3 \ldots w_n\) be a string over \(\Sigma\). Define a sequence of states \(r_0, r_1, \ldots r_n\) as follows:

• \(r_0 = q\) (the start state)
• \(r_{i+1} = \delta(r_i, w_i+1)\) for \(i = 0, 1, \ldots, n-1\)

If \(r_n \in F\), then \(M\) accepts \(w\).

If \(r_n \not\in F\), then \(M\) rejects (or does not accept) \(w\).

The language accepted by a machine \(M\) is the set of all strings accepted by the machine: \[ L(M) = \{w: \text{ w is a string over $\Sigma$ and $M$ accepts $w$}\} \]

Do Exercises Part A and B

Big Questions, and Spoilers

What languages can and cannot be accepted by a DFA?

Not all. For example: \(L = \{\epsilon, ab, aabb, aaabbb, aaaabbbb, \ldots\}\)

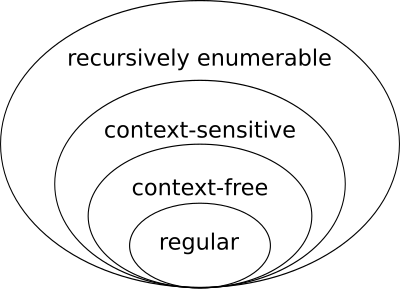
What we’re going to see when all is said and done is that different languages live at different places in what is called the Chomsky Hierarchy:

The most restrictive class in the hierarchy is the regular languages, which can be accepted by DFAs. From there, each level of the hierarchy is a more general class of languages, each of which contains all the langauges from the lower levels. Additionally, we have different types of automata that accept each language, and also ways of constructing, specifying, or describing those languages. An abridged summary:

• Regular languages can be accepted by DFAs and also NFAs; we can describe them with regular expressions.
• Context-free languages can be accepted by Pushdown Automata, and are described with context-free grammars.
• Context-sensitive languages can be accepted by Linear Bounded Automata, and are described with context-sensitive grammars
• Recursively enumerable languages can be accepted by Turing Machines, and can be described with unrestricted grammars.

Regular Operations on Languages

Definition: a language \(A\) is called regular if there exists a DFA \(M\) such that \(A = L(M)\).

How can we characterize which languages are regular?

From the Exercises, we now know that the following languages are regular, because we built DFAs for them:

1. \(L = \varnothing\)
2. \(L = \{\epsilon\}\)
3. \(L = \{s\}\) for any \(s \in \Sigma\).

Next, we’ll describe some operations that we can use to build languages from other languages. We will eventually see that regular languages are closed under these operations; in other words, if the input language(s) are regular, then the languages resulting from the following regular operations are also regular.

Regular Operations

• The union of two languages \(A\) and \(B\) is defined as \(A \cup B = \{w : w \in A \text{ or } w \in B\}\).
• The concatenation or product of two languages \(A\) and \(B\) is defined as \(AB = \{ww' : w \in A \text{ and } w' \in B\}\).
• The closure or star (or Kleene closure) of a language \(A\) is defined as: \(A^* = \{u_1 u_2 \ldots u_k : k \ge 0 \text{ and } u_i \in A \text{ for all } i = 1, 2, \ldots, k\}\)
  • In other words, it’s the language containing all possible concatenations of any choice of 0 or more strings over \(A\). Notice that 0 is an option here, so \(\epsilon \in A^*\) for any language \(A\).
  • Another equivalent recursive definition is:
    • Let \(A^0 = \{\epsilon\}\)
    • Let \(A^k = AA^{k-1}\)
    • \(A^* = \bigcup_{k=0}^{\infty} A^k\)

Theorem: The set of regular languages is closed under the regular operations.

Proof: Not yet. We don’t have the tools to prove this in full yet, but we’ll work through an example of how this can be shown for the union operation:

Consider the following two languages \(L_A\) and \(L_B\) over \(\Sigma = \{0, 1\}\):

• \(L_A = \{w : |w| \text{ is even} \}\)
• \(L_B = \{w : w \text{ ends with a $1$} \}\)

First, to prove that these languages are regular, we can show that there exist DFAs \(M_A\) and \(M_B\), where \(L(M_A) = A\) and \(L(M_B) = B\).

We did this in the Exercises!

Then, to show that \(L_A \cup L_B\) is regular, we must show that there exists a DFA \(M_{A \cup B}\) such that \(L(M_{A \cup B}) = L_A \cup L_B\).

Brainstorm: How could we do this?

(See the handwritten notes for the example DFA accepting \(L_A \cup L_B\))

The general procedure is this:

• The set of states is \(Q_A \times Q_b\)

• The start state is the state \((q_A, q_B)\)

• The accept states are \(\{(s_A, s_B) : s_A \in F_A \text{ or } s_B \in F_B\}\)

• The transition function is defined by:

  • \(\delta_{A \cup B} ((s_A, s_B), x) = (\delta_A(s_A, x), \delta_B(s_B, x))\)

    In other words, the transition function takes you from the pair of states you’re at to the pair of states the two individual machines would be in after they each saw the next symbol.

So we’ve seen that the union of two regular languages is a regular language.

Proving this property for concatenation and the closure (star) operations is a little trickier, so we’re going to take a detour that will make it much simpler: next we’re going to introduce nondeterministic finite automata, which are much easier to work with and combine. Then, the plot twist is that NFAs aren’t any more powerful than DFAs - meaning that anything an NFA can do, a DFA can also do.