As we discussed last time, the theory of computation studies computability and complexity, both of which relate to whether and how efficiently a computer can solve a certain (class of) problems.
To study these, we need to formalize and define what we mean by both of these things: computer and problem.
We saw an example of a state machine, a kind of automaton that determines its state in response to some inputs, and reaches an “accept state” depending on its inputs. Automata like these comprise our mathematical model(s) of computers, and we’ll see several types of automata with varying levels of computational power.
To formalize our notion of problems, we will focus on a particular form of problem of language acceptance. Informally, this means that a machine will be able to process a sequence of characters (a string) and determine whether it belongs to a certain family of strings (a language).
For example, a machine might be designed to “accept” strings representing binary numbers that are odd (i.e., they end in the digit 1). In our toll gate example, the automaton accepts the language of strings representing sequences of coins that add up to at least \(15\textcent\).
This may seem restrictive, and in some sense it is. However:
Let’s now get more formal about what these machines can do; we will abstract away the specifics of the problem by rephrasing it in terms of the language accepted by the machine. Some definitions:
Do Exercises Part A
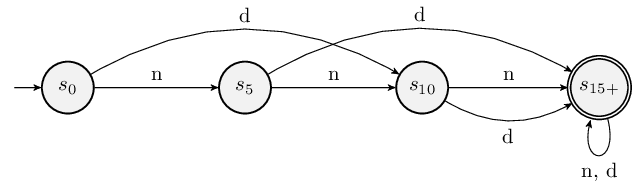
Given this, let’s formalize our toll gate automaton a bit. Here’s a diagram, where the input coins are represented as \(n\) (nickel) for a \(5\textcent\) coin and \(d\) (dime) for a \(10\textcent\) coin:

Let’s formally define the category of machines of which this state machine is an example.
A finite automaton (FA) is a 5-tuple \(M = (Q, \Sigma, \delta, q, F)\), where
Let’s map this definition onto the machine above:
Let’s look at the transition function now, which encodes the arrows in the diagram. It maps:
We can recall the transition function \(\delta\) is a function, which is a relation, which is a subset of \((Q \times \Sigma) \times Q\), so we could write it out as a set. Written out in set notation this would be a set whose first 3 elements are \(\{((s_0, n), s_5), ((s_0, d), s_10), ((s_5, n), s_10), \ldots\}\); the set has 8 elements but I’m too lazy to write them all out. Since this is tedious, we can also write \(\delta\) as a table:
n d
s0 | s5 s10
s5 | s10 s15
s10 | s15+ s15+
s15+| s15+ s15+Here’s more definition.
A finite automaton is deterministic if \(\delta\) is a function; this means that if the machine is in state \(r\) and reads input \(a\), then \(\delta(r, a)\) sends the machine to exactly one new state. Later we’ll see nondeterministic finite automata, which loosen this requirement.
Do Exercises Part B
Informally: a finite automata accepts a string if the automata can begin in the start state and process each symbol in the string and end in an accept state.
Formally:
Definition: Let \(M = (Q, \Sigma, \delta, q, F)\) be a finite automaton and let \(w = w_1 w_2 w_3 \ldots w_n\) be a string over \(\Sigma\). Define a sequence of states \(r_0, r_1, \ldots r_n\) as follows:
If \(r_n \in F\), then \(M\) accepts \(w\).
If \(r_n \not\in F\), then \(M\) rejects (or does not accept) \(w\).
The language accepted by a machine \(M\) is the set of all strings accepted by the machine: \[ L(M) = \{w: \text{ w is a string over $\Sigma$ and $M$ accepts $w$}\} \]
Do Exercises Part C