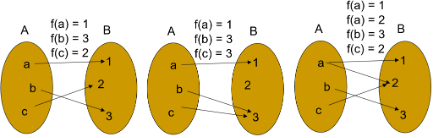
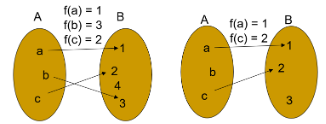
For the five relations pictured in each of the following diagrams, determine whether it’s a function or not.
There are four different functions \(f: \{a, b\} \rightarrow \{0, 1\}\). Draw a diagram for each one. Diagrams will suffice.
Let the function \(f : \{a, b, c\} \rightarrow \{1, 2, 3\}\) be \(\{(a, 1), (b, 1), (c, 2)\}\). What are the domain, codomain, and range of \(f\)?