CSCI 301 L18 Worksheet

Lecture 18 - Exercises

Part A - Relations

Let \(A = \{1, 2, 3\}\).

1. Write the relation representing \(=\) on the set \(A\); write your answer in set form.

2. Draw a diagram representing the relation \(\le\) on \(A\).

3. Write the relation representing “has the same parity as” on \(A\); write your answer in set form.

4. Consider the relation \(R = \varnothing\) on \(A\). Draw a diagram representing this relation.

Part B - Properties of Relations

1. Determine which of the following relations on the set \(A = \{a, b , c\}\) is reflexive.

   1. \(R=\{(a,a),(b,b), (c,c)\}\)
   2. \(R=\{(a,a), (c,c)\}\)
   3. \(R = \{(a,a),(b,a), (a,c),(c,a), (b,b), (c,c)\}\)
   4. \(R = \varnothing\)

2. Determine which of the following relations on the set \(A = \{a, b , c\}\) is symmetric.

   1. $R={(a,b),(b,a), (a,c),(c,a), (b,c), (c,b)} $
   2. \(R=\{(a,b),(b,a), (a,c),(c,a)\}\)
   3. \(R=\{(a,a), (b,b), (c,c)\}\)
   4. \(R = \varnothing\)

3. Determine which of the following relations on the set \(A = \{a, b, c\}\) is transitive.

   1. \(R=\{(a,b),(b,a), (a,c),(c,a), (a,a), (b,b), (c,c)\}\)
   2. \(R=\{(a,b),(b,a), (a,c),(c,a), (a,a)\}\)
   3. \(R=\{(a,a),(b,b), (c,c)\}\)
   4. \(R= \varnothing\)

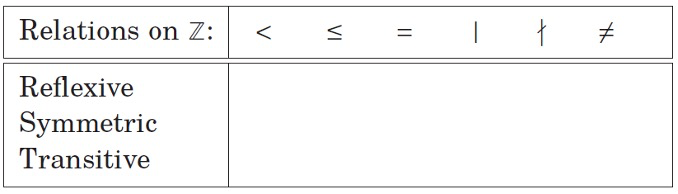
4. Fill in the following table regarding relations on \(\mathbb{Z}\):