Conjecture: The sum of the first \(n\) odd natural numbers is \(n^2\). In other words: \[ \sum_{i=1}^{n} 2n-1 = n^2 \] Is this true? It checks out for the first few values of \(n\):
\(1 = 1^2\)
\(1 + 3 = 2^2\)
\(1 + 3 + 5 = 3^2\)
But is it always true? What we’re trying to prove is an infinite sequence of statements \(S_i\), where
\(S_0: 1 = 1^2\)
\(S_1: 1 + 3 = 2^2\)
\(S_2 : 1 + 3 + 5 = 3^2\)
…and so on, including \(S_k\) for any \(k \in \mathbb{N}\).
Induction is recursion’s mathematical sibling. Here’s an argument:
\(S_0\) is true because \(1 = 1^2\).
Suppose \(S_k\) is true, meaning that \(1 + 3 + \ldots + 2k-1 = k^2\). Add \(2k + 1\) to both sides, yielding \[ 1 + 3 + \ldots + (2k-1) + (2k+1) = k^2 + 2k + 1 \] Factoring the right-hand side, we have
\[ 1 + 3 + \ldots + (2k-1) + (2k+1) = (k + 1)^2 \] Therefore, the sum of the first \(k+1\) odd numbers is equal to \((k+1)^2\).
We have shown that if \(S_k\) is true, then \(S_{k+1}\) is true. \(\blacksquare\)
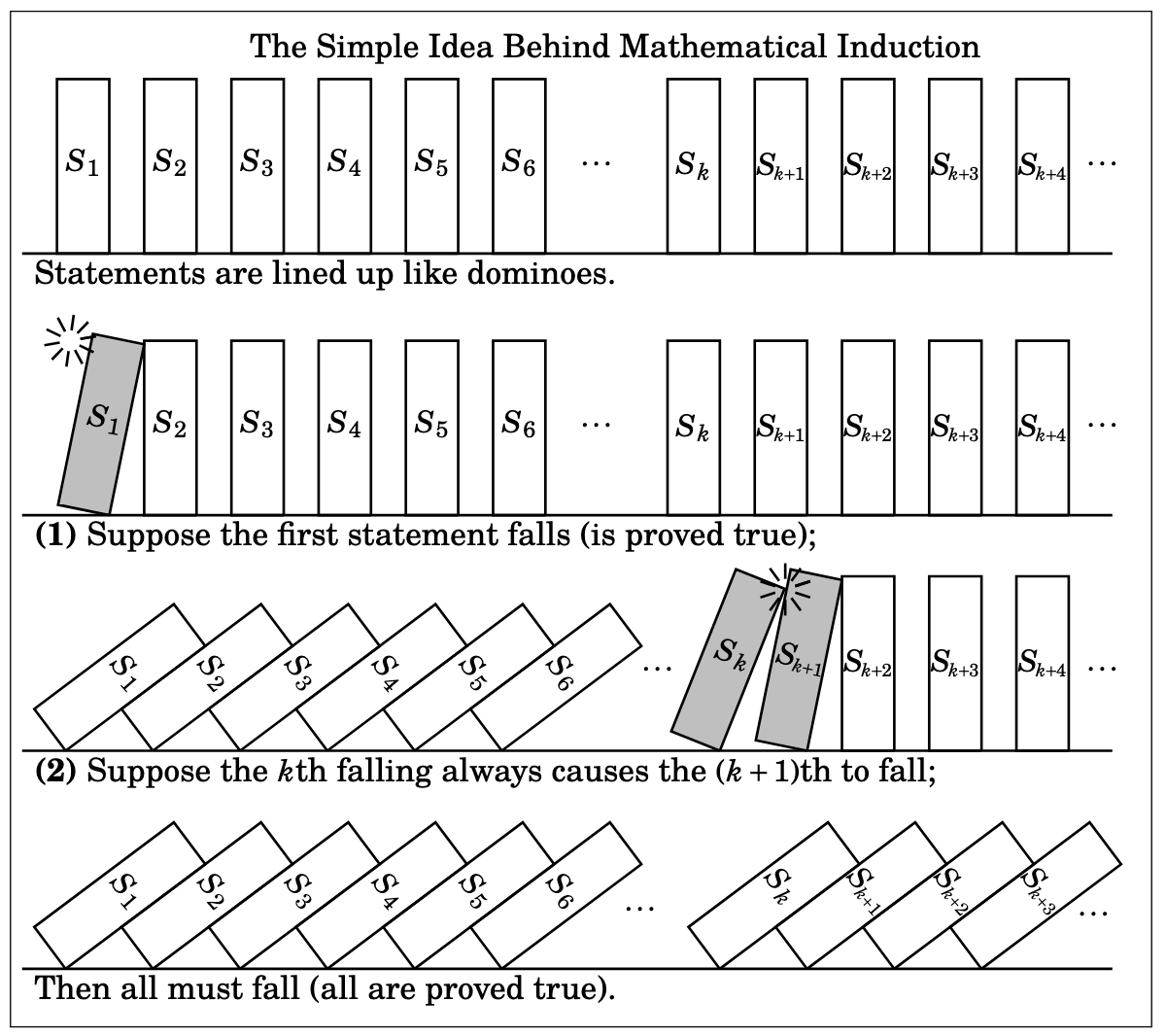
An analogy for why this makes sense is dominoes: if you’ve lined them all up so each one knocks the next one over, all you need to knock them all over is to knock over the first one:

\(S_0\) is true, because \(1 = 1^2\).
This is called the base case. It’s analogous to the base case in a recursive function or definition. This is showing that “the first domino falls”.
Suppose \(S_k\) is true
This is called the inductive hypothesis. This is saying “if we knock the \(k\)th domino over…”
At this point, all we need is to show that \(S_k \Rightarrow S_{k+1}\); in doing so, we complete the inductive step, or the inductive case. To do this is to complete the above sentence with “… then the \(k+1\)th domino falls as well.”
The standard inductive step is to show \(S_k \Rightarrow S_{k+1}\). But if we need to, we can prove $S_{k+1} using the fact that not only has the prior domino fallen, but all dominoes before it have fallen as well. In other words, a valid induction step is also to show that: \[ (S_0 \land S_1 \land S_2 \land \ldots \land S_k) \Rightarrow S_{k+1} \] This is called strong induction.
The Fibonacci sequence is defined as follows: \[ \begin{align*} F_0 &= 1\\ F_1 &= 1\\ F_n &= F_{n-1} + F_{n-2} \end{align*} \]
This is a combination of proof by induction and proof by contradiction. The basic idea is to show the base case holds, then prove the inductive hypothesis by contradiction. You can do this by supposing that it does not always hold that \(S_{k-1} \Rightarrow S_{k}\). We let \(k\) be the smallest example for which this is the case, and thus suppose \(S_{k-1}\) is true but \(S_k\) is not; then show that this leads to a contradiction.