Definition: Given integers \(a\) and \(b\) and \(n \in \mathbb{Z}\), we say that \(a\) and \(b\) are congruent modulo \(\mathbf{n}\) if \(n \mid (a - b)\). We write this as \(a \equiv b \pmod{n}\). If \(a\) and \(b\) are not congruent modulo \(n\), then we write \(a \not\equiv b \pmod{n}\).
Do Exercises Part A
Recall set builder notation, where we define a set in terms that look like: \[ \{ x : P(x)\} \] where \(P(x)\) is a “membership test”—we can now recognize as an open sentence—that must be true for \(x\) for \(x\) to be part of the set.
To prove that \(a \in \{x : P(x)\}\), then it suffices to show that \(P(a)\) is true.
We also sometimes see sets built like this: \[ \{ x \in S : P(x)\} \] To prove that \(a \in \{ x \in S : P(x)\}\), we need to show both that \(a \in S\) and \(P(a)\).
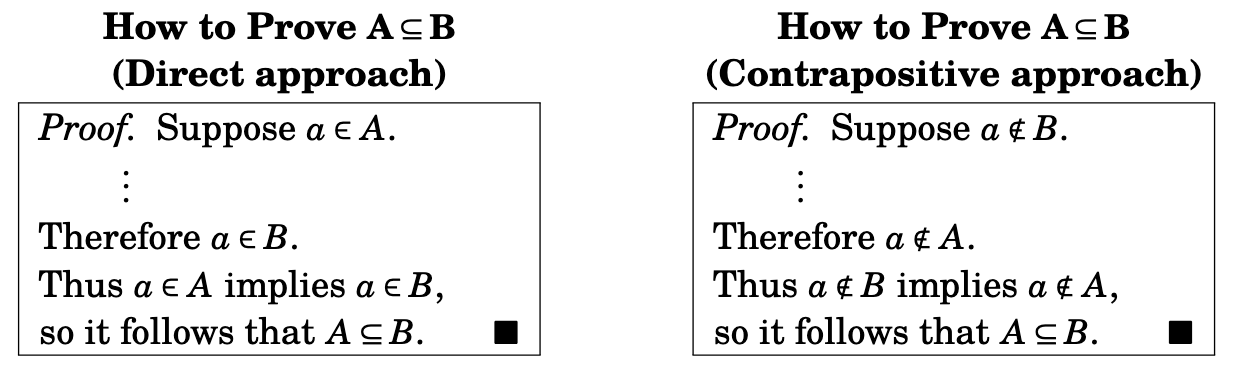
Recall the definition of subset: \(A\) is a subset of \(B\), written \(A \subseteq B\), if \(\forall a \in A, a \in B\). Therefore to prove that \(A \subseteq B\), we must show that \(\forall x \in A, x \in B\), or in other words, \(x \in A \Rightarrow x \in B\).
We can prove this directly or using the contrapositive:

The standard procedure for proving \(A = B\) is to show that \(A \subseteq B\) and \(B \subseteq A\). In other words, an element \(x\) is a member of \(A\) if and only if it’s a member of \(B\) as well.
Occasionally it’s possible to directly show the logical equivalence of the membership tests for \(A\) and \(B\).
Example: (8.1, p163) Suppose \(A, B,\) and \(C\) are sets, and \(C \ne \varnothing\). Prove that if \(A \times C = B \times C\), then \(A = B\).
Proof: Suppose \(A \times C = B \times C\).
First, we will show \(A \subseteq B\). Since \(C \ne \varnothing\), there is some element \(c \in C\). So for any \(a \in A\), \((a, c) \in A \times C\) by the definition of the cartesian product. Since \(A \times C = B \times C\), this means \((a, c\)) is also in \(B \times C\); again by the definition of the cartesian product, this means that \(a \in B\). This shows that for any \(a \in A\), we have that \(a \in B\), so \(A \subseteq B\).
Next, we show that \(B \subseteq A\); the argument is nearly the same, with the roles of \(A\) and \(B\) reversed. For any \(b \in B\), we have that \((b, c) \in B \times C\), meaning that \((b, c) \in A \times C\), and thus \(b \in A\). This shows that any \(b \in B\) is also a member of \(A\), therefore \(B \subseteq A\).
Since we have shown that \(A \subseteq B\) and \(B \subseteq A\), this completes the proof that \(A = B\). \(\blacksquare\)