CSCI 301 L05 Worksheet

Lecture 5 - Exercises

Part A - Complement, Venn diagrams

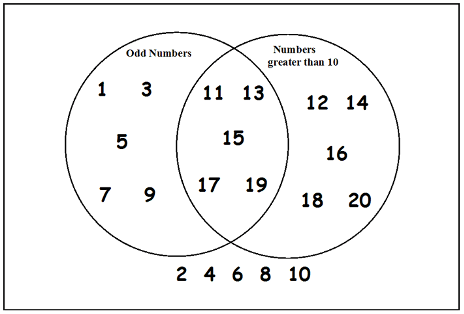
In the Venn diagram above,

Let \(U\) = \(\{x : x \in \mathbb{N} \text{ and } x \le 20\}\) be the contents of the rectangular box.

Let \(A = \{x : x \in U \text{ and } x \text{ is odd}\}\) be the contents of the left circle.

Let \(B = \{x : x \in U \text{ and } x > 10\}\) be the contents of the right circle.

List the contents of each of the following, and draw a picture of a Venn diagram with the area corresponding to that set shaded (no need to list the set elements in your diagrams).

  1. \(A \cup B\)
  2. \(A - B\)
  3. \(\overline{B}\)
  4. \(\overline{(A \cup B) - (A \cap B)}\)

Consider the following two Venn diagrams, which depict 3 sets, \(A\), \(B\), and \(C\):

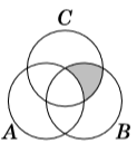
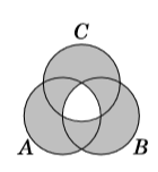
Write an expression corresponding to the shaded area in:

  1. The left diagram
  2. The right diagram

Part B - Statements

Decide whether or not each of the following is a statement. If it is a statement, say if it is true or false, if possible. 1. Every real number is an even integer.
2. Sets \(\mathbb{Z}\) and \(\mathbb{N}\) are infinite. 3. Either \(x\) is a multiple of \(8\), or it is not. 4. If the integer \(a\) is a multiple of 6, then the integer \(a\) is even. 5. \(x\) is a multiple of 8

Part C - Logical Operators (and, or, not)

Let:

and evaluate the following statements. You may find it helpful to draw a truth table for the more complicated expressions:

  1. \(N \land P\)
  2. \(Q \land S\)
  3. \(Q \lor N\)
  4. \(\neg P\)
  5. \(P \land (Q \lor S)\)
  6. \(N \land P \land Q\)
  7. \(\neg N \lor \neg Q\)
  8. \((N \lor P) \land \neg(Q \land S)\)

Part D - Conditional and Biconditional Statements

  1. Give the truth value of each of the following conditional statements:
    1. If the moon is made of green cheese, then 1 = 2.
    2. If 1 = 1, then the moon is made of green cheese.
    3. If 1 = 1, then 30 = 30.
    4. If 1 = 1, then 30 = 12.
    5. If 1 = 2, then 30 = 30.
    6. If 1 = 2, then 30 = 10.
  1. Without changing their meanings, convert each of the following sentences into a sentence having the form “If P, then Q”:
    1. Whenever people agree with me I feel I must be wrong.
    2. An integer is divisible by 8 only if it is divisible by 4.
    3. You fail only if you stop writing.
  2. Fill out a truth table with the following five columns: