Week 1 survey: fill out after you’ve completed Lab 1 and A1 (includes estimate of hours spent); due Monday night.
A2 - not ready to release it tonight; will be out no earlier than Monday. Details TBD.
When talking about a set \(P\), it’s often useful to talk about it in terms of a universal set \(U\), where \(P \subseteq U\), where \(U\) is (informally) the set of all things that might have been considered for membership in \(P\). Notice that this is informal and context-dependent, but useful nonetheless:
If talking about the set of prime numbers, then \(\mathbb{N}\) makes for a natural universal set.
If talking about odd numbers, then \(\mathbb{Z}\) makes for a natural universal set.
If talking about the set of students enrolled in this class, the universal set might be all CS premajors, or all students taking classes in CSE departments, all Western students, or all university students in the USA.
Definition If \(A\) has a universal set \(U\), then the complement of \(A\), denoted \(\overline{A}\), is the set \(\overline{A} = U - A\).
Examples:
If \(E\) is the set of even numbers with universal set \(\mathbb{Z}\), then \(\overline{E}\) is the set of odd numbers.
In our Exercises Part C, we can consider \(U\) to be the universal set for \(A\) and \(B\), so \(\overline{A} = \{2, 4, 6, \ldots, 20\}\).
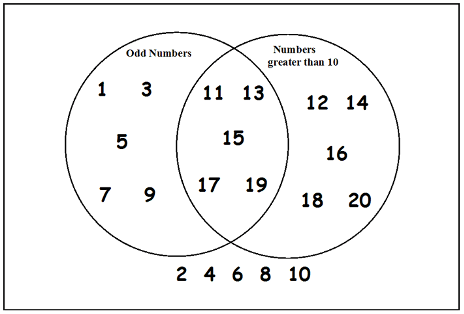
Venn Diagrams are a useful way to visualize sets and their relations with each other:

Here,
Let \(U\) = \(\{x : x \in \mathbb{N} \text{ and } x \le 20\}\) is the contents of the rectangular box.
Let \(A = \{x : x \in U \text{ and } x \text{ is odd}\}\) is the contents of the left circle.
Let \(B = \{x : x \in U \text{ and } x > 10\}\) is the contents of the right circle.
\(A \cup B\) is the contents of both circles.
\(A \cap B\) is the contents of the region where the circles overlap.
Do Exercises Part B
Definition: A statement is an English sentence or mathematical expression that is either definitely true or definitely false. That is, a statement has a definite truth value (true or false).
Switched to ipad notes from here - see whiteboard notes.