CSCI 301 L04 Worksheet

Lecture 4 - Exercises

Part A - Subsets and Power Sets

1. Let \(A = \{a, \varnothing\}\). True or false:
   1. \(a \in A\)
   2. \(\{a\} \in A\)
   3. \(a \subseteq A\)
   4. \(\{a\} \subseteq A\)
   5. \(\varnothing \subseteq A\)
   6. \(\{\varnothing\} \subseteq A\)
   7. \(\{\varnothing\} \in A\)
2. Compute the power set of each of the following sets:
   1. \(\{1, 2\}\)
   2. \(\{1\}\)
   3. \(\varnothing\)
   4. \(\{1, \{2\}\}\)
   5. \(\{\varnothing\}\)
3. [Challenge Question] If \(|S| = n\), what is \(|\mathcal{P}(S)|\)?

Part B - Cartesian Product

Let \[ \begin{align*} A &= \{a, b\}\\ B &= \{1, 2, 3\}\\ C &= \{4\}\\ D &= \varnothing \end{align*} \]

1. What is \(C \times A\)?
2. What is \(D \times B\)?
3. What is \(|A \times B|\) in terms of \(|A|\) and \(|B|\)?
4. What is \(B \times C \times D\)?

Part C - Union, Intersection, Difference

Let \(U\) = \(\{x : x \in \mathbb{N} \text{ and } x \le 20\}\)

Let \(A = \{x : x \in U \text{ and } x \text{ is odd}\}\)

Let \(B = \{x : x \in U \text{ and } x > 10\}\)

1. List the elements of \(A \cap B\).
2. List the elements of \(B - A\)

Part D - Complement, Venn diagrams

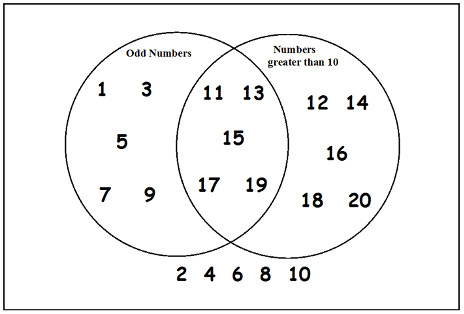
Using the sets defined in Part C and pictured in the Venn diagram above, list the contents of each of the following, and draw a picture of a Venn diagram with the area corresponding to that set shaded (no need to list the set elements in your pictures).

1. \(A \cup B\)
2. \(A - B\)
3. \(\overline{B}\)
4. \(\overline{(A \cup B) - (A \cap B)}\)